1 引言
电力市场辅助服务中的电压管理和无功控制及其定价对电力公司的运行和经营具有重要意义。目前，国内外关于无功的定价研究尚未有成熟的理论，传统的无功管理方法(如功率因数惩罚等)并不利于无功市场的形成和发展。因此，为适应电力市场发展的需要，对无功的管理及定价进行较为深入的研究是势在必行的。
Baughman、Siddiqi[1]用修正目标的最优潮流来求解各节点的实时有功和无功电价，但无功电价的模型较粗糙。文[2]引用文[1]中无功电价的表达式求得各无功补偿点的实时无功电价的变化部分，再考虑无功补偿装置的投资，从而求得各无功补偿点的总的实时电价。文[3]的作者第一次提出了发电无功成本的概念，并将其作为安全约束最优潮流的目标函数。文[4]在计算无功电价时考虑了用户对电价的响应和负荷的功率因数，其电价为有功、无功一体化模型，但目标函数中没有考虑无功发电成本和网损对无功价格的影响。以上这些无功电价，都是基于经济学方法的边际成本理论。文[5]提出了一种依据无功容量的无功定价方法，分为依据运行标准的无功定价和依据区域无功市场的无功定价，这两种定价方法的结合可作为一种很有实用前景的无功定价算法。
本文提出一个考虑系统电压静态稳定性、区域无功备用要求和无功固定投资回收的实时无功电价模型，用户无功电价包括实时容量电价和边际运行电价。其中无功容量电价基于用户的实时无功容量需求，而边际运行电价基于系统有关无功的边际运行成本[6]。在算法的设计中，提出了用分解型并行遗传算法求解目标函数极值的问题。
2 几个相关概念
2.1 静态电压稳定裕度
目前，国内外对电压失稳／崩溃和无功功率之间的关系虽然尚无统一的认识和结论，但电压稳定和无功问题是有密切联系的。系统在无功充足、线路负载较轻的情况下，一般不会发生电压失稳问题，而在局部无功短缺，缺乏足够的无功旋转备用时，就可能出现电压崩溃。本文首次在无功定价模型中引入电压稳定裕度约束，从而在电价模型中考虑了电压稳定性对无功电价的影响，使无功定价模型得到完善。
2.2 无功容量需求因子
无功服务与有功服务有明显不同，无功价格中容量价格占很大比重，且用户的无功容量需求随系统运行状况变化而变化。通常，用户的无功容量需求和其无功负荷大小是不同的。为了确定用户无功容量价格，有必要得到其无功容量需求的信息，对于基本负荷点，其无功需求与它在系统中的位置有关；对于输电交易，与交易的接受点有关。本文在文[5]的基础上，提出了一种简便可行的实时无功容量需求计算方法。
定义系统中任意节点 的无功容量需求因子(Reactive Power Demand Factor)Fi为
式中 Δqi 为母线i 处的单位无功负荷增量；QLoss为系统无功网损；k 为对应负荷功率因数的比例系数。Fi 反映了母线i 处增加单位无功负荷需要系统提供的无功， Fi 值越大，说明该节点无功越欠缺，
相应的无功容量价格分量就越高，越有利于鼓励市场参与者投资于无功建设。
2.3 无功生产维护成本
本文将无功生产维护成本引进实时无功电价的原始模型，无功生产维护成本用二次函数表示[7]
式中 
反映了无功生产中不随出力变化的部分，如部分人工成本和启动费用等； 
反映了随出力呈线性增加的部分无功生产成本，如燃料费用等；
则反映与无功出力没有很明显数量关系的无功生产维护成本，如无功生产的机会
成本等。
在实际运用中，式(2)并不需要将无功源的生产维护成本真正细分，可以采用经验或者拟合的方法得到。
3 无功实时电价模型
为简化叙述，以下模型中均省略了时段t标志，本文无功资源优化配置目标函数为(假设系统中平衡节点编号为1)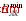
为各无功源的生产维护成本，见式(2)；NQ 为无功源个数，包括发电机和无功补偿源；B(QL) 为所有用户与消耗无功有关的净收益，无具体的表达式；QL 为负荷无功向量，模型约束条件如下：
(1)无功平衡约束(N为节点号)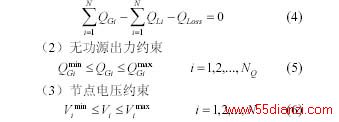
(4)变压器变比约束(Nl为装设有载调压变压器的支路数)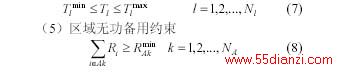 
式中 NA 为系统中区域数； 为第k 个区域最低无功备用要求；Ri 为区域Ak 中节点i的无功备用容量，具体表达式如下(fi 为i节点无功源的最大备用系数，可由系统根据系统运行水平和各区域的特点而定)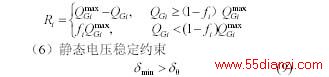
式中 δmin 为收敛潮流的雅可比矩阵的最小奇异值[8]，表示系统电压静态稳定裕度；δ0 为系统在特定时段、给定运行方式下所要求的电压静稳裕度。相应的无约束增广拉格朗日目标函数为
式中 
分别为反映各约束条件的拉格朗日乘子。
根据拉格朗日函数求极小值原理，有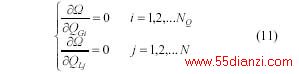
由式(10)和(11)推得
根据实时电价理论，可得用户无功边际电价为
本文关键字：暂无联系方式电工入门，电工技术 - 电工入门
上一篇：绝缘油微水测试技术
