利用小波包变换实现电力系统谐波分析
薛 蕙,杨仁刚,罗 红
(中国农业大学电气信息学院,北京 100083)
POWER SYSTEM HARMONIC ANALYSIS USING WAVELET PACKET TRANSFORM
XUE Hui,YANG Ren-gang,LUO Hong
(Electrical Engineering and Information School, China Agriculture University, Beijing 100083, China)
ABSTRACT: Using wavelet package transform (WPT) constructed on the basis of wavelet transform, the frequency band of signals can be uniformly divided and the signal features in time domain and frequency domain can be better extracted, so WPT possesses better performance for harmonic analysis. However, with the commonly used implementation method of WPT, the decomposed frequency sub bands of the signal are not arranged according to the frequency value of the sub bands, therefore, it brings disarray in signal processing. According to the sampling theorem and the implementation of filter bank, the character of frequency band division by WPT is analyzed and a new WPT algorithm for power system harmonic analysis is put forward. It is verified by practical examples that the new WPT decomPOSTTTION structure possesses better performance.
KEY WORDS: Wavelet packet transform;Harmonic analysis;Uniform frequency subband division
摘要:小波包变换(WPT)建立在小波变换的基础上,可以实现信号频带的均匀划分,能够更好地提取信号的时频特性,具有更好的谐波分析特性。但是现有的小波包变换算法实现的频带划分不是按频率大小顺序排列的,给系统和谐波分析带来混乱。根据采样定理和滤波器组实现电路分析了小波包变换实现频带划分的特点,并利用改进的小波包变换实现算法进行系统分析,实例验证这种新的小波包分解结构对谐波分析具有更好的特性。
关键词:小波包变换;谐波分析;均匀频带划分
1 引言
随着大量电力电子器件和非线性元件的应用,电力系统中的谐波污染越来越严重,越来越复杂,利用传统的傅立叶变换已不能满足实际谐波检测的需要,小波变换因其良好的时频局部化特性,可以同时提取信号的时频特性,克服了傅立叶变换时域无局部化特性的缺点,适用于非整次谐波的分离和突变谐波的检测,是一种良好的时频分析工具,在电力系统的谐波分析﹑电能质量监测中得到了广泛的应用[1-4]。但是小波对信号频带的划分不是均匀划分,而是具有高频频带宽而低频频带窄的特点,导致了高频信号的检测精度降低,小波包的出现很好地解决了这个问题。小波包可以实现信号频带的均匀划分,提高了信号的检测精度,但是利用现有的滤波器组结构实现小波包分解时,会遇到频带划分不按频率大小顺序连续排列的问题,频率大的谐波可能会被分解到较低的频带中,而频率小的谐波会被分解到较高的频带中,频率相近的谐波可能会被分解到相距较远的频带中,这样就无法通过小波包分解的结果直观地判断谐波的频率大小和特性,阻碍了小波包的广泛应用。
本文首先对现有的滤波器组结构及所存在的问题作了简单介绍,然后根据采样定理和小波包的滤波器组实现电路分析了频带不连续排列的原因,并利用改进的滤波器组实现电路进行谐波分析。仿真结果验证了这种改进的滤波器组结构可以实现信号频带的按频率大小顺序均匀划分,从而为谐波分析提供了一种更为简便直观的分析方法。
2 现有的小波包结构及存在的问题
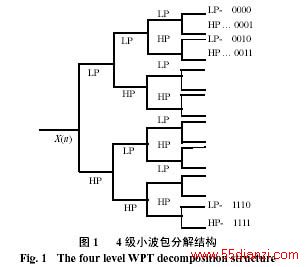
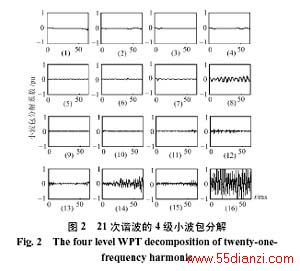
现有的小波包分解结构如图1所示,其中LP代表本节点对应一个低通滤波器,而HP对应一个高通滤波器。如果把LP记为‘0’,HP记为‘1’,则每条滤波器路径都对应一个二进制数字,依次对应十进制数中的0,1,2,3……,记为频带的标记。但是这个标记的大小与相应频带的频率大小并不是对应的关系。也就是说,低频率的信号可能会分解到标记较高的频带中,而高频率的信号可能会分解到标记较低的频带中,而且两个相邻的谐波常常会分解到不相邻的频带中。因此给谐波的频率分析、特征提取带来混乱。例如对于谐波信号分别对应21次、31次谐波分量的信号做4级小波包分解。图2是21次谐波的小波包分解,图3是31次谐波的小波包分解。图2和图3中的16个子图对应小波包分解的16个频带,按从左到右的顺序排列。由图可以看出21次谐波的能量主要集中到第16个频带中,而31次谐波的能量主要集中到第9个频带中。这样就不能够根据小波包分解结果直观地判断谐波频率的大小,给谐波的分析带来混乱和不便。

3 小波包理论分析[5, 6]
3.1 WPT原理
为解决上一节中所遇到的问题,需要从理论上分析小波包变换的实现算法。小波包变换建立在小波变换的基础上,可以简单定义为:

式中 h0和h1相当于长度为2N的低通和高通滤波器,因此小波包变换可以通过滤波器电路来实现。
3.2 WPT的滤波器组实现电路
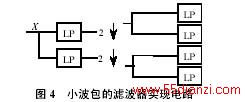
利用滤波器组实现WPT变换的过程分析如下:被分析信号通过低通和高通滤波器h0、h1后,信号频带被划分为低频和高频两个频带,然后低频和高频信号做向下采样处理,通过下一级滤波器组,不断重复这个过程,最后整个频域被划分成均匀的频带。这个分解过程可以用小波包分解树来表示,如图4所示。
3.3 采样定理
向下采样环节是滤波器组实现算法的重要部分,利用离散傅立叶变换(DFT)分析信号通过向下采样后所得信号与原来信号的关系如下。
原来信号的DFT变换满足以下的公式: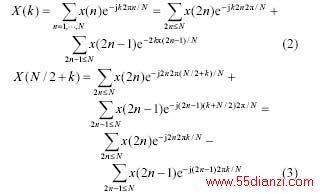
向下采样后,得到的新的序列x′(n)=x(2n) ,其中2n<N ,其傅立叶变换X′(K) 为:
![]()
根据离散傅立叶变换的对称性,在傅立叶变换序列X(k)中,X(N/2-k)的绝对值等于X(N/2+k)的绝对值。根据Naquist采样定理,如果信号的采样频率为w,则X(k)的有效频率范围为(0,w /2)。向下采样后,相当于信号的采样频率降低了一半,所以X′(K) 的有效域为(0,w/4),因此,当k<w/4时,X′(K)=0.5X(k) ,当k>w/4时,X′(K)=0.5X(w/2-k) ,对于两个谐波信号x1、x2,频率分别为w1、w2,如果频率满足w1+w2=w/2,则这两个信号通过向下采样后得到的信号的傅立叶变换值是相同的,因此可以判断向下采样后,得到的波形是相同的,例如图5,采样频率为64Hz,对于2Hz和30Hz谐波,分别向下采样后得到的波形是相同的。
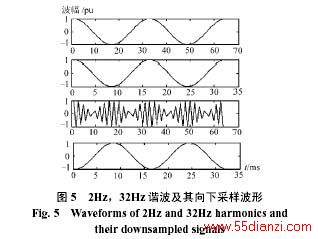
由图5中可以看出,低频信号经过向下采样后,频率不变;高频信号经过向下采样后,转化为低频信号,其频率相当于w/2-k(采样频率为w ,信号频率为k),图5的结果与上述推导一致。验证了上述推导的正确性。在此基础上可以分析小波和小波包的分解过程。采样频率为w 的信号,可检测频带为(0,w/2),在小波包变换中,通过一级镜像滤波器后,整个频带被划分为高频频带HP(w/4,w/2)和低频频带LP(0,w/4),LP信号(0,w /4)经向下采样后频率不变,经过下一级滤波器分解,这个频带又被划分为两个频带LP(0,w/8),HP信号(w/8,w/4),同时对HP信号做的向下采样处理,使HP信号(w/4,w/2)转化为频带为(0,w/4)的信号,然后通过下一级镜像滤波器,频带被分解为(0,w/8)和(w/8,w/4)两个频带,分别对应原来信号中的(3 w/8,w/2),(w/4,w3/8)频带的信号,这样就实现了高频频带的二进划分。不断重复低频和高频频带的二进划分,就可以实现频带的均匀细分。但是从上述的分析中可以看出,在现有的滤波器组结构下得到的频带划分不是按顺序连续划分,低通滤波器对应的可能是高频信号,而高通滤波器对应的可能是低频信号,例如在通过第一级滤波器组后,高频信号通过向下采样,根据以上规则,较高的频率转化为较低的频率,较低的频率转化为较高的频率,这样通过下一级低通滤波器的信号就对应原来信号中的较高频率,而通过下一级高通滤波器的信号对应原来信号中的较低频率。
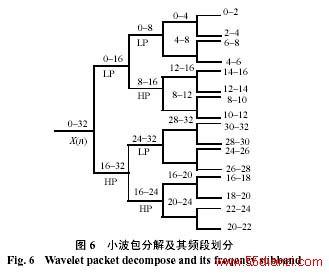
图6是一个4级的小波包分解结构及对应的频带划分情况,由图6可以观察到,在现有的滤波器组结构下,小波包分解得到的频带不是按照频率大小的顺序连续排列,而是无明显规律排列。为解决这一问题,本文利用改进的滤波器组结构来实现小波包变换。
本文关键字:谐波 电工文摘,电工技术 - 电工文摘