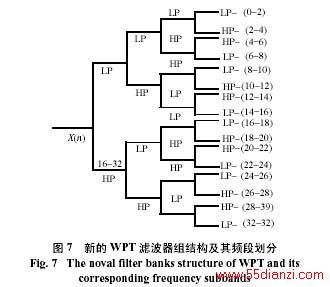
5 利用改进的滤波器组实现电路进行谐波分析
本文利用改进的滤波器组结构实现谐波信号的小波包变换,选用的基本小波是db8小波。仿真证明了利用改进的滤波器组结构实现小波包变换可以得到按频率大小顺序连续分布的均匀频带,因而比利用原有结构实现的小波包分解具有更好的谐波分析特性。
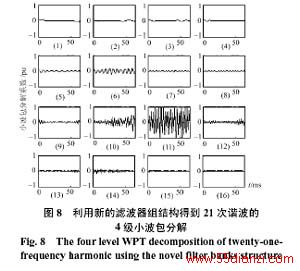
例1 被采样信号是21次谐波信号,利用原有的滤波器组结果实现的4级小波包分解如图2所示,谐波能量主要位于第16个频带,而利用改进的小波包分解结构得到的结果如图8所示,可以看到谐波能量正好位于第11个频带中,这样通过小波包的分解就可以直接判断谐波的频率对应(20,22)次谐波范围内。
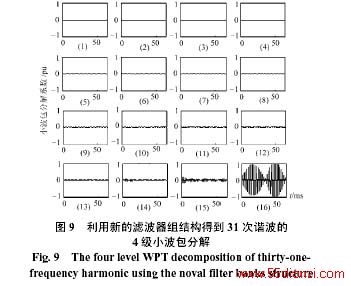
例2 被采样信号是31次谐波信号,利用原有的滤波器组结果实现的4级小波包分解如图3所示,谐波能量主要位于第11个频带,而利用改进的小波包分解结构得到的结果如图9所示,可以看到谐波能量正好位于第16个频带中,这样通过小波包的分解就可以直接判断谐波的频率对应(30,31)次谐波范围内。
从上述的两个例子中可以观察,利用改进的小波包分解结构可以为谐波频率的判断带来方便,同时,利用改进的小波包分解结构可以更好地突出被检测信号的特征。
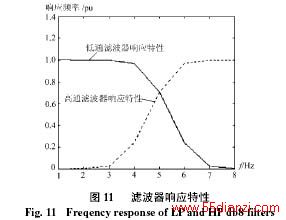
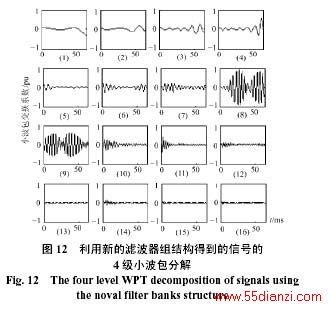
例3 利用原来的滤波器组结构,15次谐波的小波包分解如图10所示,图10中的能量主要分布在两个频带中,这是由滤波器响应不理想导致的。图11是db8小波对应的低通和高通滤波器的响应特性,当信号的频率位于两个滤波器的边界上时,信号的分解能量就同时出现在低通和高通两个频带中,利用原来的滤波器组结构,因为频带排列不是连续的,频带的进一步划分可能会导致这两个分量位于相距较远的频带中,直接观察,很难判断这究竟是两个谐波的分解结果,还是滤波器的边界效应造成的。而利用新的小波包分解滤波器组结构,得到的信号能够主要分布在两个相邻的频带中,如图12所示,因此可以判断这很有可能是滤波器的边界作用造成的一个谐波的分解情况。

6 结论
本文分析了小波包变换的实现算法及存在的问题,在此基础上利用改进的滤波器组实现算法进行谐波分析。通过实例验证了利用改进的滤波器组结构能够实现频带按频率大小顺序连续划分,从而能够直观的描述谐波的频率并能更好地提取信号的特征,是一种较好的系统和谐波分析工具。
本文关键字:谐波 电工文摘,电工技术 - 电工文摘