1 引言
次同步振荡(Subsynchronous Oscillation,SSO)一直是电力系统规划和运行中的一个重要问题。自1970年和1971年美国Mohave电厂先后两次发生由SSO引起的大轴损坏事故以来,人们对SSO问题进行了深入的研究,并提出了一系列措施来减轻其危害[1]。
目前,对多机电力系统SSO问题的研究普遍采用的方法是只保留待研究的发电机组,而将系统中其它机组进行等值简化,通常将这些机组表示为电压源与电抗(一般为该机组的次暂态电抗)串联组合的形式[2-5],从而将原系统简化为单机系统来进行SSO的稳定性分析。虽然这种简化方法得到了广泛应用,但其理论依据不足,因为该方法假设系统中其余发电机组的轴系动态特性并不会改变待研究机组的SSO特性。本文将在前人研究工作的基础上,着重阐明在何种条件下上述假设成立,并归纳了各种运行条件下系统简化的基本原则。
2 电气耦合对机组轴系扭振特性的影响
研究单机系统的SSO问题时,通常用不同数目的质量块来表示机组轴系,并引入弹性系数与阻尼系数来表示不同质量块之间的相互联接关系。具有M个质量块的轴系有M个振荡模式,其中包括一个刚体模式和M-1个扭振模式。对于刚体模式,轴系中所有质量块的振荡幅值近似相等并始终保持同相位;而对于扭振模式,其扭振自然频率互不相同。M个质量块分别不同程度地参与各个模式的振荡。
多机系统的SSO问题,最早是于20世纪70年代在美国Mohave电厂被发现的[6]。在对该电厂的两台标称相同的发电机进行SSO测试时,在其中一台发电机上意外地发现了所谓双谐振尖峰现象(Double Resonance Peak),即在机组的扭振自然频率30Hz(独立运行)附近分别出现了频率为30.07Hz和30.16Hz的两个幅值近似相等的谐振分量。Robert T.H.A.等人首先对该现象做了细致的研究并得出了一系列重要结论[7],他们认为当 台标称以及运行状态完全相同的发电机联接到共同的交流母线时,如果每台发电机的轴系都用M个集中质量块来表示,则该系统共有N´M个振荡模式,所有振荡模式可表示为式(1)所示的矩阵形式。
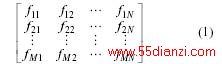
式中模式fi1(i=1,2...,M) 为第i 行中频率最低的振荡模式,对应于该 个振荡模式,台发电机组中对应质量块的振荡模式完全一致,表现了机组作为一个整体对系统的振荡特性,称之为共模(Common Modes);另外的 个振荡模式按行分为组,每一组中各个模式对应的特征相量(即模态)线性无关,因此称之为异模(Anti Modes),异模反映了发电机之间的振荡特性,每组振荡模式中的 个异模的扭振频率相同。
以同一电厂中电气距离临近的两台发电机为例,假设它们的额定值和出力完全相同,而且相对于无穷大母线的电气联接也是对称的。若每台机组的轴系均由高压缸(HP)、中压缸(IP)、低压缸A(LPA)、低压缸B(LPB)以及发电机(GEN)等5个集中质量块组成,则单独运行时的振荡模式包含一个刚体模式(扭振频率为1.67Hz)和4个扭振模式(扭振频率分别为16.35Hz、24.1Hz、30.3Hz及44.0Hz)。当两台发电机联接在一起时,对应于单机的每个振荡模式,在电气耦合作用下系统将派生出一对振荡模式,即共模和异模。如图1所示[8],对应于单机扭振自然频率为16.35Hz的振荡模式,系统派生出了模式1(共模)和模式2(异模)。另外几个单机扭振模式所对应的共模、异模与图1所示类似。
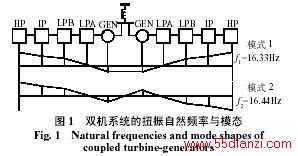
当并列运行的发电机组通过外部电气网络联接在一起时,可以认为电气网络的这种联接耦合作用与机组轴系质量块之间的弹性耦合作用是等效的。因此在进行系统SSO分析时,可以定性地认为不同机组的机械质量块是通过电力弹性联接在一起的,因此并列运行的机组必然会通过电气耦合而相互作用。从弹性系数角度讲,在电气联接对称的情况下,机组之间电气耦合越强,则相互之间的扭振相互作用也就越明显。通常,对于同一电厂中的不同机组,其等效电气耦合系数在数值上比轴系质量块之间的弹性耦合系数低一个数量级[8]。
由以上分析可知,完全相同的机组并列运行时,机组之间是存在相互作用的。但完全相同的发电机只是一种理想化的假设,暂且不论由制造工艺带来的误差,即使参数完全相同的发电机组,其负荷水平的差异也会使发电机之间的电气耦合不再对称。这种情况下的振荡模式仍然可用式(1)表示,每组振荡模式仍含有一个共模,系统中所有发电机对该模式的振荡保持同相,但振荡幅值略有差别;而其余 个异模的频率此时不再相等[7,9],相互之间存在很小的差别,机组间的扭振相互作用因频率的偏差而减弱,但这个差值很小,因此机组间的相互作用仍然比较明显[9]。
3 机组扭振自然频率与机组扭振相互作用的关系
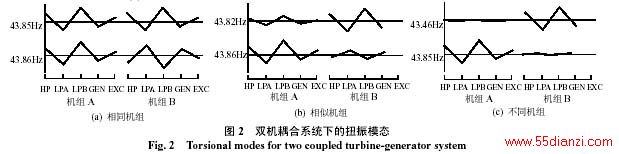
发电机的轴系参数直接影响其动态特性[10]。针对同一电厂中的发电机组,Walker D.N. 等人在文献[9]中讨论了发电机参数变化时机组间扭振相互作用的性质。如文中所述,完全相同的两台发电机组A和B,其轴系均由5个集中质量块组成,且其第4振荡模式的自然频率为43.85Hz,当机组A和B通过电气系统耦合在一起时,对应于该振荡模式,耦合系统会派生出一对与之相对应的振荡模式,其振荡频率分别为43.85Hz(共模)及43.86Hz(异模),对应的模态如图2(a)所示。由图2(a)可见,对应两个扭振模式,两台发电机组振荡的幅值是相等的。如果不考虑发电机B的励磁机质量块(EXC),则此时机组B的第4振荡模式频率变为43.82Hz,与机组A的43.85Hz的自然频率之间存在0.03Hz的差别。当两台机组耦合后系统对应扭振模式的自然频率分别为43.82Hz和43.86Hz,其相应的模态如图2(b)所示,与图2(a)相比,由于模式自然频率之间差值增大,机组之间的扭振相互作用已经变得相当弱。如果在此基础上再次修改机组B的轴系参数(弹性系数或阻尼系数),使其轴系自然频率降为43.45Hz,而机组A的自然频率保持43.85Hz不变,则机组A、B耦合后系统的自然频率为43.46Hz和43.85Hz,相应的系统模态如图2(c)所示。可见,此时机组B只参与了频率为43.46Hz的振荡,而机组A也仅仅参与了频率为43.85Hz的振荡,换言之,此时机组A和B之间几乎不存在扭振相互作用。
4 适于研究SSO问题的系统简化基本原则
复杂电力系统中发电机组数目庞大,因此在进行SSO分析时通常需将其简化为单机系统,简化的原则就是机组间不能存在扭振相互作用。本节将主要讨论如何对复杂电力系统中的发电机组进行等值简化。
首先,讨论机组轴系自然频率不同时的系统简化问题,因为电力系统中绝大部分机组都属于此类。首先假设两台发电机位于同一电厂,电气联接对称且机组负荷水平相同,由第3节讨论可知,如果机组自然扭振频率不同,那么当两台发电机耦合在一起时,机组之间的扭振相互作用将大幅减小。如图2(b)、(c)所示,0.03Hz的自然频率差值使得机组之间的扭振相互作用非常小,当频率差值增大到0.4Hz时,在系统中几乎检测不到机组间的扭振相互作用,并列运行的发电机只参与自身的振荡,其扭振特性几乎与单机运行时一致。对于系统中不属于同一电厂的发电机,如果某机组轴系参数不同,则相互之间也不会存在扭振作用。基于以上事实,EPRI建议在分析复杂电力系统的SSO问题时,如果其它发电机与待研究的发电机之间对应的自然频率差值超过 ,则可以在系统中只保留待研究的发电机,而将其它发电机用各自的次暂态电抗和固定电压源代替[4]。这样,复杂的电力系统就简化为一个单机系统,而适用于分析单机系统的SSO问题的方法较多,如频率扫描法[11]、特征值法[12]以及复转矩-测试信号法[2,13],在此不再赘述。
如果不属于同一电厂的两台发电机组轴系参数完全相同,那么它们之间也不存在明显的扭振作用,这是因为一方面它们之间的电气距离较远,因此机组之间通过电气网络形成的“等效弹性”联接作用较弱,另一方面,对于不同电厂中的发电机组,其电气网络不再对称,这都使得耦合系统的扭振频率相差较大,因而机组间的扭振相互作用变得很弱[9]。如果轴系参数相同的发电机组位于同一电厂,而且电气联接对称,运行状态也完全相同,那么它们将平均分摊外部电气系统产生的电气负阻尼,EPRI曾建议此时也只保留待研究发电机组,而将其它相同发电机等值为固定电压源[4],但这种处理方式得到的结果明显偏于保守,因为如此一来,待研究机组就要独立承担系统的所有电气负阻尼。另一种等值方法是将所有强耦合的相同机组等值为一台机,从而将整个系统等值为单机系统。Jennings G.D.等人于1986年对相同发电机组的等值问题进行了可行性研究
本文关键字:暂无联系方式电工文摘,电工技术 - 电工文摘
上一篇:有源电力滤波器主电路研究