(2-4)
H(p)称为响应y(t)对激励f(t)的传输算子或转移算子，它为p的两个实系数有理多项式之比，
其分母即为微分方程的特征多项式D(p)。H(p)描述了系统本身的特性，与系统的激励和响应无关。
这里指出一点：字母p在本质上是一个微分算子，但从数学形式的角度，以后可以人为地把它看成是
一个变量(一般是复数)。这样，传输算子H(p)就是p的两个实系数有理多项式之比。
例2-1 图2-3(a)所示电路。求响应u1(t),u2(t)对激励
的传输算子及u1(t),u2(t)分别对i(t)的微分方程。
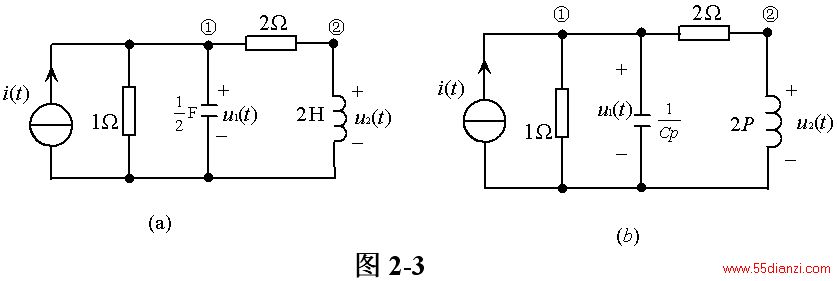
解 其算子形式的电路如图2-3(b)所示。对节点①，②列算子形式的KCL方程为
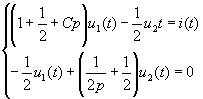
代入数据得
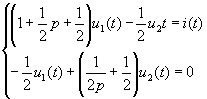
对上式各项同时左乘以p，并整理得
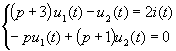
用行列式法联解得
故得u1(t)对i(t)，u2(t)对i(t)的传输算子分别为
进而得u1(t),u2(t)分别对i(t)的微分方程为
即
可见，对不同的响应u1(t),u2(t)，其特征多项式 
都是相同的，
这就是系统特征多项式的不变性与相同性。
