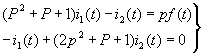
(2-2)
用行列式法从式(2-2)中可求得响应i1(t)为
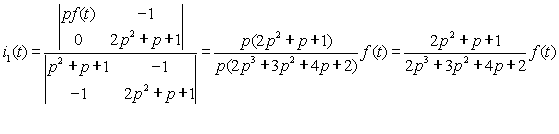
注意,在上式的演算过程中,消去了分子与分母中的公因子p。这是因为所研究的电路是三阶的,
因而电路的微分方程也应是三阶的。但应注意,并不是在任何情况下分子与分母中的公因子都可消去。
有的情况可以消去,有的情况则不能消去,视具体情况而定。故有
![]()
即
![]()
即
![]()
上式即为待求变量为i1(t)的三阶常系数线性非齐次常微分方程。
方程等号左端为响应i1(t)及其各阶导数的线性组合,
等号右端为激励f(t)及其各阶导数的线性组合。
利用同样的方法可求得i2(t)为
![]()
即
![]()
即
![]()
即
![]()
上式即为描述响应i2(t)与激励f(t)关系的微分方程。
推广之,对于n阶系统,若设y(t)为响应变量, f(t)为激励,如图2-2所示,则系统微分方程的一般形式为
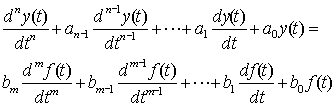
(2-3)

用微分算子![]() 表示则为
表示则为
或写成
![]()
又可写成
![]()
式中
![]()
称为系统或微分方程式(2-3)的特征多项式;
![]()