
2.2.3IDCT的实现
IDCT变换(离散余弦反变换),其计算可用下面的公式表示为:

为其他情况时,C(u)=C(v )=1。直 接按照上面的公式计算,将会有很大的运算量,势必影响JPEG的解码速度,为此可以将二维 的IDCT分为2个一维的IDCT,转换如下:
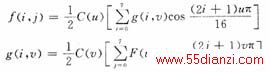
这样对8×8的二维数组进行IDCT的计算可以转化为先对该数组的行分别进行8次一维IDCT, 再对列分别进行8次一维IDCT,这样就简化了计算复杂度。下面研究如何快速实现一维IDCT 。
由文献[3]可得到8点一维DCT变换(用S8(u)表示)同16点DFT(离散傅里 叶变换,用F16(u)表示)的关系公式如下:

由上面的公式可知:对应的16点DFT的实部等于8点一维DCT变换乘以一个常数。因此,8点一 维IDCT可由16点DFT来代替。根据参考文献[3]的推导并结合ADSP的特点,8点一维IDCT可 用如下公式流程来实现:


从上面的运算步骤可以看出,一维IDCT运算已经转化成了一系列简单的加减法及与常数相乘 2.3后续处理的实现
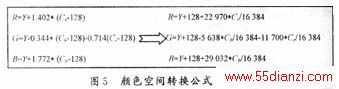
经过上述处理后,JPEG图像解码任务基本完成,但是要将解码出的图像进行显示还需要一 些后续处理。后续处理的任务之一就是完成颜色空间的转换,即将JPEG图像数据的YCbC r颜色空间转换为RGB颜色空间,其转换公式如图5左边所示。但是,为了使计算出的R , G,B的值都是正数,需要对Y,Cb,Cr分别加128进行修正,同时该公式中乘法运算出现 了浮点数 ,故需要对浮点数进行定标处理。此处,参与乘法运算的浮点数定为Q14,为了使乘法运算 的结果能直接参与加减运算,还需要将积再除以214。因此,图5左边的公式就需要转 变成右边的公式。从公式中可以看出:每计算出一对R,G,B数据,需要一对Y,Cb,Cr 数据参与运算,但是一个MCU计算出的Y,Cb,Cr数据是4∶1∶1的关系,为此,在 进行颜色空间转换前,需将1个Cb和1个Cr数组扩展成4个Cb和4个Cr数组。完成颜色 空间的转换后,再将计算出的R,G,B数据按显示设备要求的格式排列,就可以显示图像 了。的乘法运算。简化了IDCT运算的复杂度,并大大降低了运算量。用ADSP实现上面的运算,要 注意结合ADSP自身的特点,以上述第(3)步计算b3,b4为例,ADSP实现代码如下 :
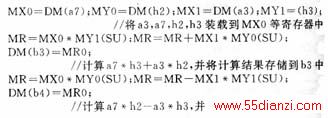
上述代码利用了操作数的特点,合理调整了各公式数据的计算次序并选用合适的指令,使一 次装载的4个数据可以完成乘、加、减三种运算,节约了指令周期。


3结语
本文以上述算法和流程为基础,在ADSP的开发环境Visual DSP下,实现了JPEG的解码算法, 并进行了优化,其中,消耗程序存储器2 566 B,数据存储器893 B。图6是原始JPEG图像, 图7是采用上述算法流程,在ADSP中进行解码后得到的BMP图像。对本算法进行适当的修改, 就可以应用到数码相机、PDA等多种嵌入式系统中。
本文关键字:暂无联系方式综合-其它,单片机-工控设备 - 综合-其它