发电机组汽门的新型非线性PID控制器的设计

　摘　要　文章基于非线性跟踪微分器、非线性度变换以及PID校正的思想，构造了一种新的非线性PID控制结构。该方法解决了一般非线性PID控制器参数整定的难题，结构简单，易于实现，鲁棒性强，又克服了由于常规PID受模型线性化的限制而使稳定范围变小，微分信号提取困难等缺陷。数值仿真结果表明，该非线性PID控制器控制品质好，有利于提高电力系统的稳定性。

　　关键词　汽门控制　非线性PID控制　跟踪微分器　非线性度

A NEW NONLINEAR PID VALVE CONTROLLER OF GENERATOR

Zhu Faguo　Yao Yubin　Chen Xueyun
Harbin Institute of Technology
Harbin，150001 China

　　ABSTRACT　This paper proposes a new nonlinear PID model of valve controller based on nonlinear tracking-differentiator，nonlinear norm and PID adjustor. The new controller is as simple and easy to realize as the linear PID controller, and exists better response and robustness than that in linear PID controller. Digital simulation result indicates that the new nonlinear controller is satisfied for improvement of power system stability.

　　KEY WORDS　valve control; nonlinear PID controller; tracking-differentiator; nonlinear norm

1　引言

　　发电机的汽门控制是提高电力系统稳定性的一种直接有效的方法。尽管现代控制理论已有相当发展，各种控制结构也应运而生，但由于其对系统数学模型的要求较高而使其应用受到了较大的限制。在控制领域中，经典PID控制方式目前仍然被广泛使用。电力系统是一个复杂的大规模非线性系统，强非线性和结构的多变性是其两个主要特点。常规PID控制器无法满足电力系统稳定性控制的要求。文献［1］基于非线性跟踪微分器和非线性组合的思想，设计了具有强鲁棒性和非线性适应能力的非线性PID控制器，在应用中显示了很好的效果，但其结构复杂，参数意义不很明确，整定较为困难。本文针对原非线性跟踪微分器产生跟踪超调和非线性组合参数整定困难的缺陷，给出了其改进模型，并运用于发电机汽门控制，获到了较好的效果。

2　非线性PID控制器

2.1　非线性跟踪微分器
　　在实际控制过程中，控制所需信号往往是不连续或不可微的，或在噪声的干扰作用下，信号变得不连续或不可微，给PID控制品质的提高造成很大的障碍，非线性跟踪微分器在积分作用下跟踪信号及其微分信号，成功地解决了这一问题。
　　文献［1］提供了二阶跟踪微分器的结构：

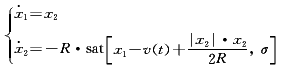
(1)

式中　R为一大于零的常数。
　　可以证明，对式（1）输入一信号v(t)，它将产生两个状态信号x1(t)和x2(t)，其中x1(t)跟踪输入信号v(t)，，即x2(t)为输入信号v(t)的广义微分信号。令为该跟踪微分器的开关平面函数。为了防止在s＝0附近出现高频颤振现象，式（1）在开关平面函数上设置了线性饱和区间(-σ，＋σ)。
　　在仿真和分析过程中发现，开关平面进入线性区后，x2的变化速度将大大减缓，若系统正处于快速跟踪阶段（即｜x2｜较大时），跟踪过程将产生较大的超调。因此，在开关平面函数中引入了罚函数e｜x2｜，得改进后的跟踪微分器结构为

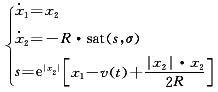
(2)

　　式（2）中R决定了系统的跟踪速度，其值取R＝4C／T2t，c为被跟踪信号幅值，Tt为跟踪微分器的跟踪时间常数，一般小于被跟踪信号周期T0的0.5倍。若被跟踪信号为非正弦信号，则可通过傅立叶分析大致得到c和T0 (T0应取最高次谐波的周期值）。δ越大，抵御干扰的能力越强，但也增大了干扰信号衰减振荡的周期，因此一般可视开关平面函数s所受干扰的大小，在满足抗干扰情况下取较小的整定值。
2.2　非线性度α变换
　　非线性度α变换，即在误差信号进入控制器前先进行幂指数为α的变换。以非线性度α＝0.5为例，对一阶系统G(s)＝1/TS的比例控制作简略分析。由图1所示结构和非线性度的定义，得出非线性调节器输出控制信号为

(3)

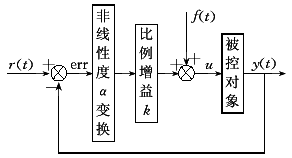
图1　非线性度α调节器
Fig.1　Nonlinear norm α regulator

　　由一阶系统输入输出关系Y(s)＝G(s)*U(s)的拉氏反变换可以发现，控制输出信号与系统输出信号满足关系

(4)

　　将式(4)代入式(3)，得系统输出的轨迹为

(5)

　　由式(5)可发现：
　　(1)在输入信号r(t)为单位阶跃信号，扰动
f(t)＝0时，系统输出误差的运动轨迹与初速度为v0＝k/T、加速度为a＝k2/2T2的物体恒减速率运动轨迹相同，系统到达稳态即err＝0的时间(称作调整时间ts)为ts＝2T/k，较之传统线性比例控制系统进入误差2%的调整时间ts＝4T/k快1倍，且在调整时间后，系统误差在非线性度变换控制下为零，即实现了真正无差调节。
　　(2)在输入信号r(t)＝0，扰动f(t)为单位阶跃函数时，系统误差的运动轨迹同样与初速度为v0＝1、加速度为a＝k2/2T2的物体恒减速率运动轨迹相同，系统在t＝2T2/k2后将进入稳态即dy/dt＝0，其误差为err＝1/k2，较之线性比例控制的稳态误差err＝1/k大大减小，即非线性变换增强了系统抗扰动的能力和自身参数的摄动性。
　　对于非线性度α(0＜α＜1)的情况，在参考输入r(t)为单位阶跃信号，系统所受扰动f(t)＝0时，非线性度α与系统调整时间ts的对应关系如表1；在参考输入r(t)＝0，外加扰动f(t)为单位阶跃输入时，系统稳态误差为。

表1　调整时间与非线性度关系表
Tab.1　Realation of adjusting time and nonlinear norm 非线性度α1.00.90.80.70.6 调整时间ts

[1] [2] [3]  下一页

本文关键字：暂无联系方式电工文摘，电工技术 - 电工文摘