谐振技术及其应用

摘要：首先介绍了硬开关电路的缺陷，引出谐振技术，然后详细分析了基本电路在不同的初始条件下的工作情况，接着分析了谐振参数间的关系及其会带来的问题。最后，介绍了该技术的应用，同时分析该技术在变换器中存在的问题。

关键词：硬开关；软开关；谐振技术

Resonant Technique and Its Application

SUN Ze, WANG Gang

Abstract:The faults of hard switching circuit are first analyzed, then the resonant technique by using a basic circuit is introduced and the relation between the resonant parameters and questions produced possibly are analyzed. At last, its application and existing questions in converter are presented.

Keywords:Hard switching; Soft switching; Resonant technique

中图分类号：TN86文献标识码：B文章编号：0219－2713(2002)3－0093－04

1  引言

    在开关电源中，通常采用磁性元件（如铁心电感、变压器等）实现交流/直流侧的滤波，能量存储和传输。这些磁性元件在电源装置的体积、重量、成本中占有很大比重。开关器件的工作频率越高，磁性元件的尺寸就可以越小，电源装置的小型化、轻量化、低成本化就越容易实现。但是，传统的PWM变换器中的开关器件工作在硬开关状态，存在很多缺陷：

    1）开通和关断损耗大；

    2）感性关断问题；

    3）容性开通问题；

    4）二极管反向恢复问题。

    由于硬开关工作时存在上述四大缺陷，所以使开关器件工作频率的提高受到限制，从而电源装置的小型化、轻量化、低成本化也就不易实现。克服以上缺陷的有效办法就是应用软开关（SoftSwitching，简称SS）技术。最理想的软开通过程是：电压先下降到零后，电流再缓慢上升到通态值，所以导通损耗近似为零。另外，因器件导通前电压已下降到零，器件结电容上的电压亦为零，因而解决了容性开通问题，这意味着二极管已经截止，其反向恢复过程结束，因此二极管反向恢复问题亦不复存在。最理想的软关断过程是：电流先下降到零，电压再缓慢上升到断态值，所以关断损耗近似为零。由于器件关断前电流已下降到零，即线路电感中电流亦为零，所以感性关断问题得以解决。事实上，这两个过程要么存在感性关断问题，要么存在容性开通问题。也就是说，仅仅利用一个电感或电容是不能根本解决问题的，所以最好的情况应当是使开关在电压和电流同时为零时关断和开通，损耗才会真正为零。而要实现这个目标，就要用到谐振技术。

2  谐振技术

2.1  谐振过程

    根据电路原理，电感电容串联或并联可构成谐振电路，使得在电源为直流电源时，电路中的电流按正弦规律变化。由于电流或电压按正弦规律变化，存在过零点，如果我们能够在这一时刻开通或关断，产生的损耗就为零。下面就分析电源里用得最多的二次串联谐振电路，对其在初始情况不同时的工作情况进行讨论。基本电路如图1所示。

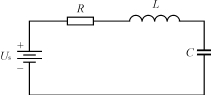
图1  基 本 二 次 串 联 谐 振 电 路

    假定电容C上的电压为uC，电感L中的电流为iL，电源电压为Us。于是，该电路的微分方程为：

    L(di/dt)＋Ri＋uc=Us    （1）

    i=C(duc/dt)           （2）

将式（2）代入式（1），得

    LC(d2uc2/dt2)＋RC(duc/dt)＋uc=Us    （3）

式（3）对应的齐次方程为：

    LC(d2uc2/dt2)＋RC(duc/dt)＋uc=0    （4）

该齐次方程对应的特征方程为：

    LCs2＋RCs＋1=0    （5）

在R<条件下，求得方程的解为：

    s1=－β＋jω′

    s2=－β－jω′    （6）

式中：β=R/2L；

    ω′=；

    ω0=。

于是，式（4）的解为：

    =e－βt(A1cosω′t＋A2sinω′t)    （7）

很显然，uc=Us是方程的一个特解，即

    =Us    （8）

可得，式（3）的通解为：

    uc=y=＋

    =e－βt(A1cosω't＋A2sinω't)＋Us    （9）

    下面分别讨论该电路在不同初始条件下的解以及相应的电压电流波形：

    1）第一种情况

    初始条件为：iL=0，uc=0。方程的解为：

    uc=－e－βtsin(ω't＋ arctan)＋Us    (10)

    iL=e－ βtsin(ω't)    （11）

波形如图2所示。

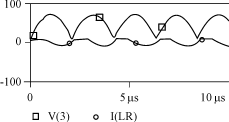
图2  初 始 条 件iL=0，uc=0时uc，iL波 形

    2）第二种情况

    初始条件为：iL=0，uc=U0。方程的解为：

    uc=e－βtsin(ω't＋ arctan)＋Us    (12)

    iL=－e－βtsin(ω't)    （13）

波形如图3所示。

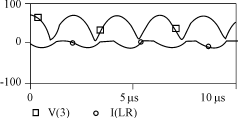
图 3  初 始 条 件iL=0，uc=U0时uc，iL波 形

    3）第三种情况

    初始条件为：iL=I0，uc=U0。方程的解为：

    uc=e－βtsin(ω't＋arctan)＋

       e－βtsin(ω't)＋Us    (14)

[1] [2]  下一页

本文关键字：技术  电工文摘，电工技术 - 电工文摘