(重庆大学电气工程学院电力系,重庆 400044)
摘 要:发输电组合系统的可靠性评估主要采用解析法和蒙特卡洛模拟法。这两个方法各有优点,但在可靠性评估过程中都要反复进行潮流计算,以判断是否违反运行约束,从而确定系统是否处于故障状态,并计算恢复策略实施过程中的负荷削减量,这将花费大量的计算时间。为改善发输电组合系统可靠性评估的计算效率,缩短评估时间,适应实时在线评估的需要,该文提出基于网流规划(NFP)的评估算法。计算结果表明,此算法是高效和合理的。
关键词:发输电组合系统;可靠性;网流规划
1 引言
电力系统的根本任务是优质、经济、安全、可靠地将电能输送给用户。因此,可靠性评估成为发电系统、输电系统、配电系统规划决策中的重要工作[1]。近年来,电力系统不断向超高压、远距离、大容量方向发展,这极大地提高了系统运行的经济性,但同时也使电力系统的安全可靠问题逐渐突出,因此,对电力系统可靠性的研究变得日益迫切。现今,我国正向电力市场迈进,电力市场中的用户在购买一定数目电量商品的同时,也购买了此商品的基本属性——“可靠性”[2];系统的可靠性也是影响实时电价的重要因素。在实时电力市场的交易中,实时电价中与可靠性有关的电价部分的计算需要进行系统可靠性的实时在线评估;同时,电力市场的出现,输电网的开放,独立发电商的出现也使系统的运行条件不能事先知道,不可避免的会导致系统运行接近物理极限[3,4],这就对电力系统的可靠性评估提出了新的要求:快速﹑准确并能适应在线评估的需要。
组合系统在电力系统可靠性评估中的两种最基本的分析方法是蒙特卡洛模拟法和解析法[5~9]。二者各有其优缺点和适用范围。解析法的主要优点是:物理概念清楚,模型的精度高。它通过枚举系统故障状态,然后对此系统状态进行潮流计算,以判断此枚举状态是否为故障状态;由于潮流计算涉及矩阵计算,计算量较大,并且随着系统规模的增大,需要枚举的系统状态呈指数增长,对每一个枚举状态都进行潮流计算将耗费大量机时,所以解析法最适合于网络规模较小而网络结构较强的系统。蒙特卡洛模拟法是统计试验方法,其统计的采样次数与系统规模无关,容易处理各种实际运行控制策略和各种随机分布,所以蒙特卡洛模拟法在进行大型复杂电力系统可靠性评估时更具有优越性;它的主要不足在于计算时间与计算精度的紧密相关性,为获得精度较高的可靠性指标,往往需要很长的计算时间;并且要对每一样本状态进行潮流计算,因此计算时间很长[10]。因此要提高可靠性计算的速度,缩短评估的时间,可以从3个方面进行研究: ① 改进故障状态筛选算法,把对指标贡献较小的事件忽略不计[11]; ② 改进事件行为分析算法,提高速度[1]; ③ 采用并行算法,在并行处理机上实现并行计算[3]。
文献[1]提出利用RBF神经网络进行故障状态的识别以加快评估过程的速度,但由于神经网络的训练过程需要花费大量的时间,并且当系统的运行方式改变或系统进行了扩建,该神经网络需要重新进行训练,因此该模型不适用于系统的可靠性实时评估。本文提出利用网流规划模型,以网流替代系统线路潮流,考虑网损和线路无功对输电线路弧的有功容量进行修正,通过系统最小割集求得系统能够提供的最大有功负荷,当此割集容量小于系统有功负荷时,认为系统处于故障状态,以此作为故障状态的筛选判据。
2 利用网流规划进行故障状态筛选的基本原理
网流规划是针对网络拓扑特性提出来的一种数学规划方法,也是线性规划中专门处理网络问题的一种特殊算法。由于该方法简单可靠,并能有效地提高解题速度,因而在电力系统输电网规划中得到了广泛应用。图1 所示的2机3节点电力系统,其网络图可以用图2来表示。
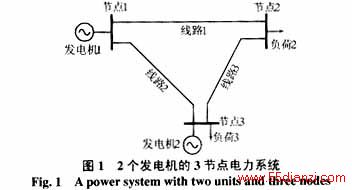
图2中节点1,2,3对应原有电力系统的母线编号;G1和G2代表发电弧,其一端连至共同的电源点S,另一端连至实际发电机所在的节点,其弧的容量为相应发电机的最大有功发电容量,它们对应的可靠性参数就等于相对应的发电机组的故障参数;E1﹑E2﹑E3代表输电线路弧,分别对应相应编号的输电线路,其弧的容量为对应线路的最大输送容量,它们可靠性参数就等于相应的输电线路的故障参数;L2和L3代表负荷弧,其弧的容量为相应母线上的有功负荷,负荷弧的一端连在负荷所在的实际母线上,另一端连至共同的收点T。
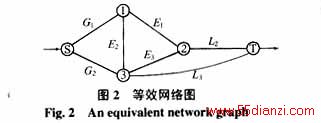
设Xij为网络中弧ij的实际流量,Rij为该弧的最大容量,E为全部弧的集合,如下的线性规划问题称为最大流问题
上述条件中ES、ET、Ei分别表示与节点S、T、i相连的弧集合,r表示发点S的净流出量(或收点T的净流入量)。
网络的最大流代表了该系统在不违反弧的容量约束和满足克希荷夫第一定律情况下,从发点S向收点T所能传输的最大流量,如果该网络代表的是电力网络,则最大流表示在线路和发电机都不过负荷的情况下,系统所能供应的最大有功负荷。由最小割集定理可知:任意网络从发点S到收点T的最大流的数值等于分离网络的最小割集容量。因此,求取原网络最大流的问题转化为其最小割集问题。
发输电组合系统的充裕度可靠性评估主要是分析系统在受到扰动后的稳态情况下,在保持电力平衡和维持母线电压在运行范围内的前提下满足用户电力及电量需求的能力。如果在某一系统状态下,网络的最小割集容量小于系统的总有功负荷,该系统一定处于故障状态,必须进行系统开机出力调整甚至负荷削减,这是本文进行故障状态筛选的基本原理。由于利用网络在特定状态下的最大流代替系统中的潮流分布,从而简化了交流潮流的计算和负荷削减计算,因此利用网流规划进行发输电组合系统可靠性评估,计算速度很快。
在以上的模型中,假定输电线路弧的容量为该输电线路的容量,由于在线路上存在网损,并且线路上不仅传送有功,而且也传送无功,因此输电线路的容量并不是该线路的最大有功输送容量,如果以线路的容量作为线路的最大有功输送容量进行故障状态的筛选,将使一些故障状态被遗漏。因此,有必要对线路弧的容量进行修正,方法如下:
设输电线路弧Xij的线路容量为Rij,由系统所有元件都处于正常状态下的潮流计算得到该线路的有功网损为△Pij,传输的无功为Qij,则修正容量R'ij为:![]()
3 可靠性评估的算法及计算结果分析
可靠性评估的算法如下:
(1)计算系统元件都处于正常状态下的系统潮流,计算线损,对输电线路弧的有功容量进行修正;
(2)枚举系统状态,判断该状态是否造成系统解列,若解列则对各个解列子网计算其各自的最小割量,否则计算该状态下整个系统的最小割量;
(3)若最小割量小于该网络的有功总负荷,则判断该状态为失效事件;
(4)对失效事件进行行为分析,计算出各个节点和系统的可靠性指标;
(5)若系统状态已经枚举完毕,则退出计算,否则转步骤(2)。
图3为IEEE-RTS24系统的结构图。本文利用解析法采用可靠性网流评估算法对IEEE-RTS24系统进行了可靠性评估,枚举系统事故状态,输电线路故障模拟到2阶,发电机故障及发电机和输电线路组合故障考虑到4阶。计算结果如表1所示。
由表1可见,网流可靠性评估的计算速度非常快,利用求取最小割量对发输电组合系统的故障状态进行筛选,特别是利用系统正常状态下的无功和线路损耗对线路容量进行修正后,能够抓住系统的主要故障状态;同时利用系统有功总负荷和最小割量的差值作为系统应该削减的有功负荷,避免了在故障状态下的调整过程中为了求取负荷削减量而反复进行交流潮流计算,从而极大地节省了评估时间。另外,从表1还可以看出,网流法计算出的指标与R.Billinton提供的指标相差很小,差异的原因在于削减负荷的策略不同,以及网流法以网流替代潮流,只满足克希荷夫第一定律,未考虑节点电压约束,即不满足克希荷夫第二定律。虽然如此,其计算精度能够满足可靠性评估的要求,并且由于评估所需时间很短,完全能够满足实时在线评估的需要。