股票价格预测被认为是当前时间序列预测中最富挑战性的应用之一。股票价格的高精度预测意味着投资者高额的回报和政府部门对市场的有效监管。因此自19世纪股票市场建立以来，股票价格预测模型就成为各国学者研究的焦点。在时间序列预测中，线形的概率统计模型曾得到广泛的应用，如ARMA模型法、AR模型法、阈值自回归、多项式自回归、指数自回归模型等，后来还有灰色预测、混沌时间序列预测及神经网络等方法，其中BP神经网络最引人注目、并且使用最多。然而，由于神经网络学习算法实际上是利用梯度下降法调节权值使目标函数达到极小，导致了神经网络过分强调克服学习错误而泛化性能不强。同时神经网络还具有一些其它难以克服的缺陷，如隐单元的数目难以确定，网络的最终权值受初始值影响大等。近年来，随着人工神经网络研究的深入，人们更加认识到它存在的严重不足，在原理上缺乏实质性的突破，同时也缺乏理论依据。总之，神经网络学习算法缺乏定量的分析与机理完备的理论结果［1］。
随着非线性理论和人工智能技术的快速发展，近年来以粗糙集（Rough set，RS）理论和支撑向量机（Support vector machines，SVM）等为代表的软计算方法已成为金融市场有力的分析和预测工具。本文分析了RS和SVM两者各自的特点，探讨了两者的结合方法，利用RS理论在处理大数据量、消除冗余信息等方面的优势，减少SVM训练数据，从而克服了SVM算法因为数据量太大、处理速度慢等缺点，提出了一种基于RS理论数据预处理的SVM预测系统。最后将该系统应用于上证股票价格预测中，与BP神经网络及标准SVM方法相比，得到了较高的预测精度，从而表明了基于RS理论的方法作为信息预处理的SVM学习系统的优越性。
1 RS理论与SVM预测原理
1．1 RS的知识约简方法
RS理论是一种新型的处理模糊和不确定知识的数学工具，能有效地分析和处理不精确、不一致、不完整等各种不完备信息，并从中发现隐含的知识，揭示潜在的规律［2］。
知识约简是RS理论的核心内容之一。人类在对一个事物做出判断和决策时，并不是依据被判断事物的全部特性，而是依据最主要的一个或几个重要特点做出判断。知识约简就是根据这一原理，剔除知识库中的冗余知识，简化判断规则。
假定人们感兴趣的对象的论域为U，论域U中的一种关系定义为R，R可以是一种属性的描述，也可以是一个属性集合的描述，可以是定义一种变量，也可以是定义一种规则。当用R描述论域U中所有等价类族时，可以表示为U｜R。若R是U上的划分，R＝｛X1，X2，…，Xn｝，（U，R）称为近似空间。用des｛Xi｝表示U上基于关系R的一个等价关系对Xi的基本集合的描述。例如，属性集A⊂R，desA｛Xi｝＝｛（a，b）：：f（x，a）＝b，x∈Xi，a∈A｝，因此这里表示对于给定的集合Xi可用属性A和属性集VA表示。
不可分辨关系是指物种由属性集P表示时，在论域U中的等价关系。例如，属性集P⊂R，对象X，Y∈U，对于每个Q∈P，当且仅当f（X，a）＝f（Y，b）时，X和Y是不可分辨的，即有
f（X，a）＝f（Y，b）｝
ind（P）的等价类称为知识P的基本概念或基本范畴。如果r∈P，且ind（P）＝ind（P－（r）），就称属性r是属性集合P中可省略的，否则称r是属性集合P中不可省略的。可以这样理解，属性r对于描述对象的特征作用不大，属于冗余属性，省略以后不会影响对象特征的描述。利用这一特性，就可以进行知识约简，从众多的特征信息中，提取有用的属性，简化处理过程［3，4］。
1．2 SVM的预测原理
SVM方法是统计学习理论（Statisticallearning theory，SLT）的一种成功实现，它建立在SLT的VC（Vapnik－chervonenkis）理论和结构风险最小化（Structural risk minimization，SRM）原理的基础上，根据有限样本信息在模型的复杂性（即对特定训练样本的学习精度）和学习能力（即无错误的识别任意样本的能力）之间寻求最佳折衷，以期获得更好的泛化能力［5］。
用SVM算法估计回归函数时，其基本思想就是通过一个非线性映射φ，把输入空间的数据x映射到一个高维特征空间中去，然后在这一高维空间中做线性回归。
给定一数据点集
，其中xi为输入向量，di为期望值，n为数据点的总数。SVM采用下式来估计函数［6］
在式（2）中，本文采用Vapnik的ε不敏感损失函数。损失函数的用途在于，它能够用稀疏数据点表现由式（1）给出的决策函数。
为了寻找系数w和b，就需要引入松弛变量ξi和
，使下式最小化
给出的决策函数就变成下面的精确形式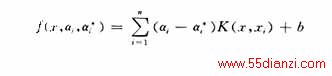
对任何i＝1，…，n都有等式αi×
＝0，αi≥0，≥0成立。要在约束条件（4）下最小化式（3），在引入拉格朗日乘子后，就可以把这一凸优化问题简化为对一个二次优化问题寻找向量w的问题，在这种情况下，要找到所求的向量
通过在二次优化方法中控制c和ε两个参数，就可以控制（即使在高维空间中）SVM的泛化能力。
根据二次规划中的库恩－塔克条件，在方程（6）中系数（αi－）只有一部分数目是非零值，它们所对应的数据点就是支撑向量。这些数据点位于决策函数的ε边界上或在边界外。在方程（6）中，由于其它数据点的系数（αi－）都等于零，从而证实了在所有的数据点中只有支撑向量能够决定决策函数［7］。
一般说来，ε值越大，支撑向量数目就越少，因而解的表达就越稀疏。然而，大的ε值也能降低数据点的逼近精度，从这一意义上讲，ε也是解的表达的稀疏程度与数据点的密度之间的平衡因子。
在式（6）中，K（xi，xj）称为核函数，核函数的值等于两个向量xi和xj在其特征空间中的像φ（xi）和φ（xj）的内积［8］，即
任何函数只要满足Mercer条件都可用作核函数，采用不同的函数作为核函数，可以构造实现输入空间中不同类型的非线性决策面的学习机器。
1．3 RS与SVM的优缺点分析及结合方法
RS是一个强大的数据分析工具，它具备以下优势：首先RS不需要先验知识。模糊集和概率统计方法是处理不确定信息的常用方法，但这些方法需要一些数据的附加信息或先验知识，如模糊隶属度函数和概率分布等，这些信息有时并不容易得到。RS分析方法仅利用数据本身提供的信息，无须任何先验知识。其次RS能表达和处理不完备信息，以不可分辨关系为基础，侧重分类；能在保留关键信息的前提下对数据进行约简并求得知识的最小表达；能识别并评估数据之间的依赖关系，揭示出概念简单的模式；能从经验数据中获取易于证实的规则知识。
本文关键字：暂无联系方式电力配电知识，电工技术 - 电力配电知识
