逻辑代数

　　逻辑代数亦称为布尔代数，其基本思想是英国数学家布尔于1854年提出的。1938年，香农把逻辑代数用于开关和继电器网络的分析、化简，率先将逻辑代数用于解决实际问题。经过几十年的发展，逻辑代数已成为分析和设计逻辑电路不可缺少的数学工具。
　　逻辑代数提供了一种方法，即使用二值函数进行逻辑运算，这样
，一些用语言描述显得十分复杂的逻辑命题，使用数学语言后，就变成了简单的代数式。逻辑电路中的一个逻辑命题，不仅包含肯定和否定两重含义，而且包含条件与结果许多种可能的组合。比如，一个３输入端的与非门存在着输入与输出状态的八种可能的组合。用语言描述既噜嗦又不清晰，用真值表则一目了然，而用代数式L＝ABC表达就更为简明。
　　逻辑代数有一系列的定律和规则，用它们对数学表达式进行处理
，可以完成对电路的化简、变换、分析和设计。

一、逻辑代数的基本定律和恒等式

常用逻辑代数定律和恒等式表：

 

                       

基本定律

加

乘

非

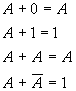
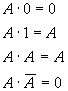
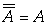
结合律

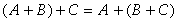
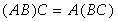
交换律

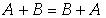
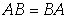
分配律

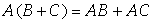
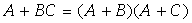
反演律（摩根定律）

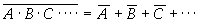
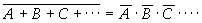
吸收律

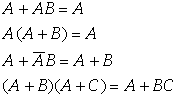
其他常用恒等式

　　表中的基本定律是根据逻辑加、乘、非三种基本运算法则，推导出的逻辑运算的一些基本定律。
　　对于表中所列的定律的证明，最有效的方法就是检验等式左边的函数与右边函数的真值表是否吻合。

例如，要证明A＋A=A时，可按照下面的步骤进行证明：
　　1. 令A＝1，则A＋A＝l＋l＝l＝A；
　　2. 令A＝0，则A＋A＝0＋0＝0＝A；
　　除此之外，别无其他可能，可见A＋A＝A。

　　恒等式可以用其他更基本的定律加以证明，我们来证明其中的第一条，即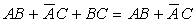

　　证明如下：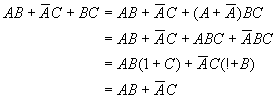

　　在以上所有定律中，反演律具有特殊重要的意义。反演律又称为摩根定律，它经常用于求一个函数的非函数或者对逻辑函数进行变换
。

[1] [2]  下一页

本文关键字：暂无联系方式电子技术，电工技术 - 电子技术