张海波，张伯明，孙宏斌，吴文传
(清华大学电机工程与应用电子技术系，北京 100084)
摘 要：提出了一种新的形成电力系统状态估计可观测岛的拓扑分析方法。该方法利用内网等值的思想隐去支路量测岛内部节点，将仅由边界节点和它们之间的岛际互连支路构成的若干待并网作为分析对象，总结了关于度1、度2节点的特殊合并规则。当量测岛互联成网状时，提出了利用潮流定解条件判定量测岛是否可合并的简单规则。文中对所提规则进行了验证并对所提方法的有效性进行了讨论。
关键词：电力系统状态估计；可观测性分析；潮流定解条件
1 引言
利用现有量测配置能够正确地计算出电网状态量的范围[1]，其算法的好坏将直接关系到状态估计的运行性能，甚至可决定状态估计软件能否顺利地运行。在某些情况下，状态估计计算不收敛是因为网络可观测性分析算法有错，而且这种情况时有发生。现有可观测性分析算法主要有两类：数值算法[2,3]和拓扑算法[4,5]，其中拓扑算法由于其计算速度快，又能够克服数值算法中易受舍入误差影响的弱点而受到许多电力研究人员的青睐，但其仍存在不尽人意之处[6]。文[6]在充分分析了支路量测岛的可观测条件的基础上，对量测岛间可合并条件进行了理论分析。本文是文献[6]的算法实现。文中通过分析给出了判断量测岛合并的4个实用判定规则，按此规则提出了一种新的电力系统状态估计可观测性的拓扑分析方法。
2 对度1、度2节点的讨论
假定2个或多个量测岛合并时，其中至少有1个是活岛，任选1个活岛作为吸入岛，其内部状态量可观测，该岛的边界节点即可看作是{U，q}已知节点，从该活岛开始合并其他量测岛，合并后的岛仍可保证为可观测岛，即活岛。下面给出几个关于节点合并的判定规则。
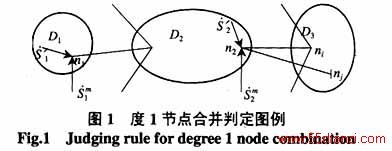
规则1 若有一边界节点的度为1，且该节点上有注入量测，则该注入量测所在的岛可以和与该边界节点相连的量测岛合并。
有注入量测的度1节点发出的岛际支路连接另一量测岛，若任意指定这2个量测岛中的一个活岛为吸入岛，则吸入岛上边界节点的电压可认为已知，待合并的2个岛中未知状态量的个数为1，即为另一岛上某一边界节点的复电压。而由度1节点注入量测恰可列出仅含这一未知状态量的注入方程，即有功和无功的注入复功率方程，此未知状态量可解。由于两岛内的量测方程足可估计两岛内的全部状态量，故两量测岛可合并。如图1所示，D1、D3为死岛，图中D2为吸入岛，节点n1、n2均为度 1节点，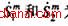
为注入量测，由于D2是活岛，其内部节点电压已知，因此，由
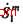的量测方程可求出节点n1的电压，进而求出D1上其他节点的电压，故D1和D2可合并。由
的量测方程可计算D3中节点ni或nj的电压，可将D2和D3合并。下面以节点n2为例，简要地分析此规则。对节点n2可列出下面的注入量测方程：
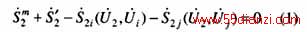
因节点ni ，nj 位于同一个量测岛上，可通过D3的内部支路潮流方程将
的函数，所以式(1)又可写成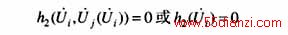
此方程可解。因此，由度1节点n2联系的2个岛可合并。
此规则对各种状态估计计算方法均能适用，也可以应用此规则合并2个死岛，但合并后的岛仍须标记为死岛，因合并后的岛内仍含有1个未知复数状态量待求。
规则2 若由度2节点相连的3个量测岛都为活岛，且度2节点有注入量测，在不采用P，Q分解法状态估计时可将这3个岛合并。
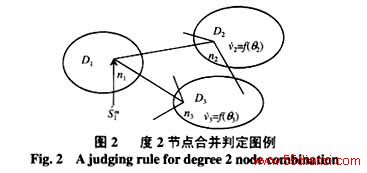
如图2所示，D1~D3均为活岛，节点n1为度2节点且有注入量测，任选一岛作为吸入岛，图中选为D1，则n1点电压{U1，q1}可看作已知量。由于D2、D3都是活岛，内部均有电压量测，相当于补充了2个关于电压幅值的方程，而电压幅值的参考点都是相对于地的，所以，若给定相角q2，则D2内状态量可求，给定相角q3，则D3内状态量可求，即3个岛内的未知状态量只有q2和q3。由节点n1的注入功率P，Q的量测方程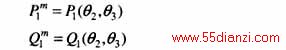
可联立求解q2和q3，这样的3个岛可合并。但当采用P，Q分解法状态估计时，由于P，Q解偶，上述2个注入功率方程不能联立求解，所以此度2节点合并方法不能适用，但可用于基本加权最小二乘状态估计和正交分解法状态估计。通过算例验证了此规则的正确性。但按此规则判定合并后的网络虽整体可观测，但由于P，Q的量测方程联系较弱，当量测条件不好时，状态估计易发散，故需视具体情况来决定本规则采用与否。
下面再分析两种度2节点合并时的特殊情况。图3中，D3和D8为活岛，箭头代表注入量测。其中, n4、n5和n10、n11分别为有注入量测的度2节点，观察他们的节点注入功率方程可以看出，由n4、n5节点的注入功率方程可解出
，即D3~D5可合并；同样，由n10、n11点注入功率方程可解出 
，即D6~D8可合并。总结这2种情况可看出，若2个度2节点的注入功率方程中仅含相同的两个复电压未知量，那么与度2节点相连的节点和这两个度2节点所在的3个量测岛可合并。由此，可得出规则3。
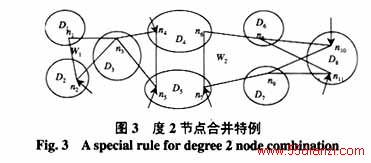
规则3 若存在2个有注入量测的度2节点，且与他们直接相连的所有边界节点所在的岛加上这2个度2节点所属量测岛的岛数仅为3，即可将这3个岛合并。此规则可用于各种状态估计算法。
需要指出的是，此规则的适用范围并非仅限于图3中的那两种特殊情况，只要这2个度2节点中每一个所建立联系的3个量测岛完全相同，就可以直接应用此规则进行判断，因为3个岛中含2个未知复电压状态量(假定为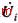
和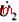
)，2个度2节点中每一组有联系的3个岛完全相同, 就可保证由其建立的2个方程中只含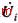和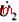这2个未知量，因此，方程可解，这样的3个岛可合并。在图3中，如果n8和n9各自分裂成2个独立的边界节点，那么，规则3对这种情况也适用。
规则3在应用时也可用于合并3个死岛，但与规则1相同，此时必须标记合并后的岛仍为死岛。规则1~3为度1、度2节点合并的判定规则，与之类似的规则也可推广到度3，度4，…，等节点，但考虑到实际中难以遇到，且会使编程复杂化。所以，本文所提算法中暂不采用。
3 利用潮流定解条件判定分裂后待并网的可观测性
利用等值方法隐去量测岛内部节点后，对无注入的边界节点按其所连岛际支路数进行节点分裂，可生成多个新的拓扑上彼此独立的无注入边界节点，此时就可由所有边界节点和连接边界节点的岛间互联支路做拓扑分析，得到若干分裂后的待并网。由于这些分裂后的待并网上不存在支路潮流量测（支路潮流量测在形成支路量测岛时已利用过了），只有注入量测，且在含有注入量测的分裂后的待并网中，所有节点电压均包含在其上有注入量测边界节点的注入量测方程中，因此，可以说分裂后待并网的可观测性分析就相当于确定该网的潮流定解问题。由于这些分裂后的待并网散布于整个网络中，彼此互不影响，故采用这种方法对化简后的待并网进行分析既可以将量测岛的合并问题简化，又避免了文献[2]中所提出的环岛判定原则从整体上考虑量测岛合并时易引起误判的问题。
要想求解一个潮流问题，至少要找到和未知状态量个数相等的独立方程数。作为吸入岛的活岛，其边界节点可作为（U，q）已知节点，考虑到编程的简化和讨论方便，以最坏的情况即子网上只有一个活岛时为例加以分析。假定分裂后待并网节点数为n，则未知状态量个数为n-1，这就要求独立方程数为n-1个，由于待并网内可能有多个边界节点在同一个量测岛上，而这些边界节点上有注入量测，因此可能产生某些局部量测冗余，而其他地方量测又不足的情况，因此还不能简单地以节点注入量测数³ n-1作为潮流定解条件。
对于和待并网在同一量测岛上的边界节点，需要区别不同情况加以分析，其中，有注入量测的点分析时可作为{P、Q}节点，而没有注入量测的节点因其电压可由内网支路潮流方程的作用表示成在同岛上{P、Q}节点的节点电压的函数，从而亦可作为{U，q}已知节点来处理。这样，就可给出分裂后待并网上潮流可解，即分裂后待并网上节点所在量测岛可合并的判定规则。
规则4 假定分裂后待并网上边界节点所在量测岛数为n，只要该网节点中有注入量测的边界节点所属的不同量测岛数³ n-1，则这n个岛可合并到其中的一个活岛上。
下面对规则4加以简要的分析证明：由量测岛的性质可知，一个量测岛内的未知状态量最多为一个复电压，在分裂后待并网所在的n个量测岛中，选定一个基准岛即吸入岛后，因吸入岛上节点电压被认为是已知量，则这n个量测岛所含未知状态量数最多为n-1个复电压。因此，只要能够找到n-1个独立复方程解出各岛上的一个复电压即可将此n个岛合并。只要分裂后待并网的边界节点中有注入量测节点所属量测岛数³ n-1，就可保证至少有n-1个独立的注入复方程，且至少n-1个岛上含有{P、Q}节点，与之同岛同分裂后待并网无注入量测的边界节点都可作为{ U,q }节点来处理。由于经过了节点分裂，这些注入量测的方程中含有分裂后待并网上所有节点的电压变量。将{U,q}节点的电压、相角方程带入到这些注入方程后，并不改变原注入量测方程组的独立性，且使方程组中的未知节点电压数恰好与独立方程数相等，因此，状态量可解，这n个量测岛可合并。
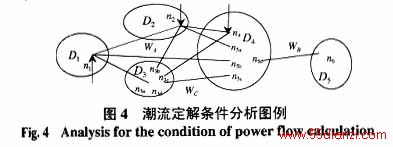
现以图4中分裂后待并网WA（包括D1~D4）为例进行分析，图中节点n5a，n5b和同岛{P、Q}节点n4在同一个分裂后待并网WA 上，节点n5a，n5b可看作{U，q}已知节点，因它们的电压均可表示为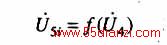
式中 i = a, b。
节点n3a，n3b，n3c的电压相等，节点n1、n2、n4有注入量测，因而可列出3个包含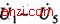
共5个节点电压的独立注入方程。n5的电压可写成 
的函数，将n5点的电压代入到n1、n2点注入量测方程后并不改变这3个注入量测方程的独立性，而未知状态量减少了一个，由5个变成了4个，在确定了平衡节点后，未知状态量个数变为3个，正好等于独立方程数，分裂后待并网WA的潮流可解，所以这4个岛可合并成一个岛。分裂后待并网WC包括D3和D4，由于2岛之间互联支路的端节点n3和n5上均无注入量测，所以不能以此判定此2岛可合并，这2个岛的合并是利用边界节点n1，n2，n4上的注入量测来实现的。分裂后待并网WB的潮流显然不可解，因此D5是不能和其他4个岛合并在一起的。
4 基于潮流定解条件的可观测岛形成方法
（1）有效性分析
本文所提方法均为从局部网络进行分析，这样可以保证合并过程的充分性，不致引起误判而造成状态估计不能进行的严重后果。但只从局部进行分析有可能会漏掉某些局部网络潮流不可解而整体网络潮流可解的情况。例如图3中的待并网W2，由2个度2节点可确定D6~D8可合并，而将节点n8，n9分裂后形成的2个分裂后待并网各自的潮流却不可解，无法利用规则4进行判别。出现这种情况的原因主要是由于不同的分裂后待并网所属的量测岛相同或重叠。因为各岛内未知状态量仅有一个复电压，这就使得这些不同的分裂后待并网的注入方程中的未知状态量相同或重叠，因此，这些不同的分裂后待并网的注入方程可联立求解。但若分析此类整体网络潮流可解而局部网络潮流不可解问题，将导致组合项过多，实施起来很困难。况且，除极个别情况外，此类问题可采用规则1、3和规则4相结合以及循环判别的方法，通过先对某个局部进行合并操作来改变其他局部的合并判别条件，从而逐个求解局部网络潮流而达到整体网络潮流可解的目的。
（2）可观测岛的形成步骤（为了算法的通用性，这里暂不应用规则2）：
1）用有量测支路形成稀疏存储的节点关联矩阵，用图的深度优先搜索的方法进行拓扑分析可得到各节点所属的不同初始支路量测岛，对于没有支路量测相连的孤立节点也要作为独立的初始量测岛处理，将有电压幅值量测的量测岛定义为活岛，无电压幅值量测的量测岛定义为死岛。步骤1）结束时，所有支路量测已利用完毕。
2）利用网络图的邻接表信息计算边界节点的度，非边界节点的度为0。扫描所有有注入量测的边界节点，利用规则1和规则3先对初始量测岛进行合并，由于量测岛合并可能使边界节点的度发生变化，此过程要循环进行，直到没有合并操作时为止。
3）对无注入量测节点做节点分裂处理，然后对由内网等值和节点分裂处理后余下的边界节点和岛际互连支路做拓扑分析（与前面形成初始支路量测岛的方法相同，只是这时是由岛际支路形成节点关联矩阵，然后再做深度优先搜索），可得到若干分裂后待并网，按规则4分别对其进行合并判断，此过程亦要循环进行，直到没有合并操作时为止。
4）再扫描一遍所有边界节点，确定没有符合规则1和规则3的节点后，统计最终形成的可观测岛，按可观测岛重新组织量测，为状态估计做准备。
按以上步骤对图3进行分析，按规则3合并后，D3~D5，D6~D8分别变成一个岛，n7点变成度1节点且有注入量测，根据规则1，合并生成的2个新岛又可合并成D9；由于n1、n3点没有注入量测，由n1、n2、n3点构成的分裂后待并网潮流不可解，不能将D1、D2、 D9合并；又因为D1、D2为死岛，最终形成的可观测岛就只有D9，它包含了D3~D8共6个岛。
5 算例分析
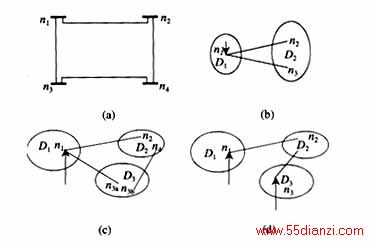
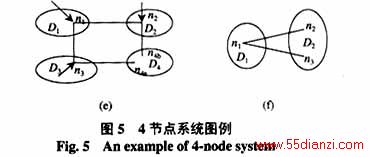
为验证本文所提的规则及本文提出的一个量测岛内最多只有一个未知复电压状态量的基本结论，对图5所示4节点系统做可观测性分析试验，其中，图5(c)中的D1~ D3均为活岛；图5(d)~(f)中的D1为活岛。
图5(a)为4节点系统，图5(b)~(f)为按表1所列配置量测时，以文[1]和本文方法处理后的结果。表1还给出了使用的规则和得到的结论。为验证判定结果的正确性，分别在对应情况下做此4节点系统的状态估计，试验证明在配置方案1~4情况下，4节点系统的状态估计均能正常运行。而在量测配置方案5时,边界节点无注入量测，不能将2岛合并，D2又是死岛，不能作为可观测岛进行状态估计，所以，在这种量测配置下，全网无可观测区域。试验表明，此种量测配置下的状态估计不能正常进行。算例说明了应用本文所提规则进行的可观测分析是正确的。
按本文算法编制的可观测性分析程序已应用于清华大学TH-2100EMS软件中，并通过多个电网实际运行条件的考验。
6 结论
本文所提可观测岛的形成方法属拓扑方法，程序简单，计算速度快，便于在线应用，且从推导过程可以看出，本方法处处注意了量测岛合并时的充分性，避免了因误判合并而造成的状态估计不可进行的严重后果。另外，本文所提分析方法对未来在边界节点上增加量测配置以扩大量测范围具有很强的指导意义。实践证明了本方法有效实用。
参考文献
[1] 王克英，穆刚（Wang Keying, Mu Gang）, 计及PMU的状态估计精度分析及配置研究（Precision on improvement and PMU placement studies on state estimation of a hybrid measurement system with PMUs）[J]. 中国电机工程学报（Proceedings of the CSEE）， 2001，21（8）：29-33.
[2] Monticelli A. Wu F F. Network observability identification of observable islands and measurement placement[J]. IEEE on PAS 1985, PAS-104(5)：1035-1041.
[3] 阎欣，单渊达（Yan Xin, Shan Yuanda）, 基矢量抽取法及可观测性分析（Base-Vector extraction method and its application in observability analysis）[J]. 中国电机工程学报（Proceedings of the CSEE）， 1999，19（4）：18-22.
[4] 邓佑满，张伯明（Deng Youman, Zhang Boming），网络可观测性的拓扑分析（Network observability topological analysis ）[J].清华大学学报（自然科学版）（Proceedings of Tsinghua University），1993、4(2)：8-13.
[5] 张伯明，陈寿孙（Zhang Boming, Chen Sousun），高等电力网络分析（Advance power system analysis ）[M].北京：清华大学出版社（Beijing：Tsinghua University Press），1996.
[6]张伯明. 电力系统状态估计可观测性分析中关于量测岛合并的理论分析(Theory analysis about measurement islands’ combination in observability analysis in power system state estimation)[J].中国电机工程学报（Proceedongs of the CSEE）,2003,23(2)：16-19.
本文关键字：潮流 电工文摘，电工技术 - 电工文摘
