Parameters Optimization for UPFC Damping Controller
Using Trajectory Sensitivity
ZHANG Lai, FANG Dazhong,YANG Xiaodong
(School of Electrical Engineering and Automation,
Tianjin University, Tianjin 300072, China)
Abstract: A new approach for optimizing the parameters of supplementary damping controller of the UPFC is proposed. In this approach, the sum of generator speed is utiliz ed as the objective function. Trajectory sensitivity analysis is performed to ob tain the sensitivity of the objective function to the controller parameters and conjugate gradient method is adopted to optimize the parameters using the sensit ivity obtained. Simulation results on the New England test system show that the suggested method can damp low frequency oscillation effectively.
Key words: unified power flow controller(UPFC); supplementar y damping controller; trajectory sensitivity; conjugate gradient optimization te chnique
1前言
三峡电站的发电运行及各大区域电网的逐步互联标志着全国性的电网即将形成。全国性电网形成后由于区域电网间的联络较弱,电力系统低频振荡将是制约区域电网间功率相互支援的主要问题之一。
灵活交流输电系统(FACTS)技术的出现为抑制低频振荡,特别是区域间振荡提供了新的手段[1,2]。统一潮流控制器(UPFC)作为最有力的FACTS设备,可以对有功功率、无功功率和电压分别控制,对于提高系统的暂态稳定性及阻尼系统的振荡具有显著的作用。为了实现UPFC抑制系统振荡的功能,人们提出在UPFC的主控制环节上附加一个控制结构类似于电力系统稳定器的控制器[3],其输出信号用于调制主控制环节的参考值。这种类型的控制器已成为UPFC和其它FACTS设备进行阻尼控制的主要方式[3,4]。
近年来,轨迹灵敏度技术被逐渐引入到电力系统分析中并在电力系统参数识别[5]和稳定性分析[6]领域得到了成功应用。文献[7]提出了一种基于轨迹灵敏度技术优化设计电力系统稳定器参数的新方法,使用该方法设计出的电力系统稳定器除了可提高系统小扰动稳定性抑制系统自发性低频振荡外,还可以有效阻尼大扰动引起的系统振荡。目前,此类轨迹灵敏度优化技术在FACTS控制器设计中的应用还未见报道。
本文提出一种基于时域仿真和轨迹灵敏度分析进行UPFC附加阻尼控制器参数优化设计的新方法。该方法将扰动后发电机转速的时域累加值作为优化的目标函数,通过轨迹灵敏度分析获得目标函数对优化参数的梯度,而后采用共轭梯度法进行参数优化设计。在新英格兰系统上的仿真结果表明了该优化设计方法的有效性。
2UPFC的主控制与附加控制
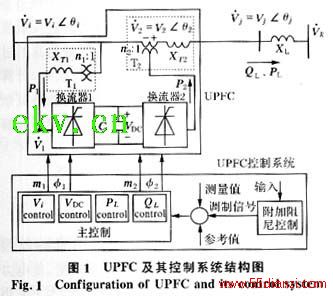
图1给出了UPFC及其控制系统的示意结构图。UPFC主要由变压器、换流器和直流电容组成。其中n1、XT1和n2、XT2分别为并联变压器T1和串联变压器T2的变比和等效电抗;m1、φ1和m2、φ2分别为换流器1和换流器2的交直流电压比和触发角,它们是UPFC的可控参数;C为直流电容,VDC表示直流电容电压;P1表示从并联侧流入换流器1的有功功率,P2表示从换流器2流入串联侧的有功功率。UPFC在动态稳定研究中常采用如式(1)所示的动态模型[8]。该模型中,交流量采用标幺值,直流量采用有名值。

2.1UPFC主控制
UPFC主控制功能包括潮流控制、直流电容电压控制和母线电压控制。UPFC的串联侧主要用于线路的功率控制。可通过串联换流器的触发角控制和电压比调节实现UPFC串联侧的线路有功控制和无功控制,如图2(a)所示;UPFC的并联侧可作为无功补偿以支撑母线电压,并且为串联侧提供所需的有功交换以维持直流电压恒定,可通过并联换流器的电压比调节实现母线电压控制,如图2(b)所示;通过并联换流器的触发角控制实现并联侧的直流电压控制,如图2(c)所示。

2.2UPFC附加控制
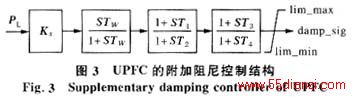
UPFC的附加阻尼控制具有类似于电力系统稳定器的结构,如图3所示。该阻尼控制器采用线路的有功功率作为输入信号;输出则作为图2(a)中的阻尼调制信号dampsig,用以调制线路功率控制的参考值,从而达到增加系统阻尼、平息持续振荡的目的。
3轨迹灵敏度分析
轨迹灵敏度分析[9]是针对微分方程模型研究状态变量对参数依赖性的方法,对稳定控制以及选取系统参数具有十分重要的指导意义。下面介绍轨迹灵敏度系统的推导过程。多机电力系统的动态模型可用一组微分代数方程描述,即
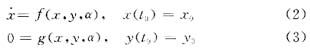
式中,x是状态变量向量;y表示代数变量向量;α是设计参数变量,在本文中α由UPFC参数Ks、T1、T2、T3、T4组成。方程组(2)-(3)的解轨迹可表示为

对微分方程(2)进行积分可以得到
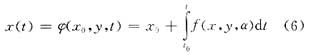
然后将式(6)对α求导数可得

因此,系统轨迹对参数在α=α0的轨迹灵敏度可以表示为
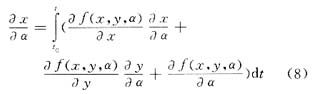
为了便于标记,分别定义系统轨迹x(t)和y(t)对参数α在α=α0的轨迹灵敏度为xα0和yα0,即
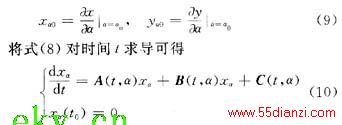
对式(3)参数α进行相似的求解过程(其中α=α0)可得
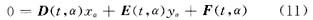
式(10)中,A(t,α)=f(x,y,α)/x,其它雅可比矩阵B(t,α)、C(t,α)、D(t,α)、E(t,α)和F(t,α)可类似表示。需要注意的是,A(t,α)、B(t,α)、C(t,α)、D(t,α)、E(t,α)和F(t,α)是时变矩阵,依赖于系统变量x和y变化。
本文将微分代数方程组(2)-(3)称为轨迹系统,而称微分代数方程(10)-(11)为轨迹灵敏度系 统。在对轨迹系统(2)-(3)进行时域仿真的过程中,可以同时对轨迹灵敏度系统进行求解,计算灵敏度信息。文献[9]提出的求解方法将轨迹灵敏度系统作为轨迹系统求解的一个副产品,使得求解轨迹灵敏度的计算量显著减少。
4UPFC参数优化
4.1优化模型
优化UPFC阻尼控制器参数的目的是使UPFC对各种机电振荡模式提供最佳阻尼,使电力系统以最快速度到达故障后稳定运行点。本文采用大扰动后系统中发电机速度轨迹来评价系统的阻尼效果。换言之,使扰动后系统中发电机速度轨迹衰减最快的UPFC阻尼控制器参数是最优的[10]。基于这种理解,本文提出如下参数优化数学模型
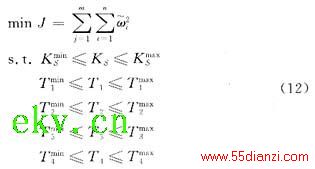
式中:n为系统中所有发电机数目;m为时域仿真的离散时间点数;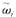 为惯性中心(center of inertia,简称COI)坐标框架[11]下发电机速度。机电仿真程序积分求解方程组(2)-(3)后可得同步坐标框架下的发电机速度变量。采用如下变换将同步坐标中的
为惯性中心(center of inertia,简称COI)坐标框架[11]下发电机速度。机电仿真程序积分求解方程组(2)-(3)后可得同步坐标框架下的发电机速度变量。采用如下变换将同步坐标中的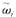 转化为惯性中心坐标下的发电机速度
转化为惯性中心坐标下的发电机速度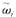 ,即
,即
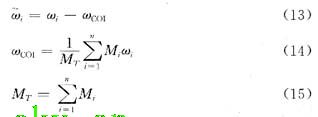
其中Mi是系统第i个发电机的惯性时间常数,ωcoi代表惯性中心相对于同步坐标框架的速度。
4.2目标函数对优化参数的梯度
优化中需要用到目标函数对UPFC阻尼控制器参数的梯度。结合电力系统时域仿真进行第3节介绍的轨迹灵敏度分析,可以获得每个仿真时间点的发电机转速ωi及其对UPFC阻尼控制器参数α的灵敏度ωai,将ωi和ωai代入式(16)即可得到目标函数对优化参数的梯度∂ J/∂α。
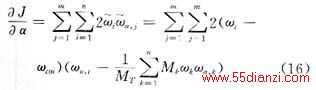
4.3约束条件的处理
令u代表所有待优化参数向量,则式(12)可简写为

本文采用三角函数非线性变换可将有约束的非线性规划问题式(17)变为无约束的非线性规划 问题。

式中bi表示向量β的第i个元素,其初始值的取值

有约束的非线性规划问题式(17)变成如式(20)所示的无约束规划问题。

4.4优化步骤
本文采用共轭梯度法求解优化问题。共轭梯度法在每次迭代步骤中将当前梯度信息和已有的搜索方向做线性结合,获得当前搜索方向,然后沿着当前搜索方向做一维线性优化,求解一维优化点的梯度信息,而后进入下一步迭代。其具体优化步骤如下:
1)设k=0,给定初始近似点α(0)及收敛精度ε;
2)进行灵敏度分析,计算g(0)=∂ J(0)/∂α(0)。





![]()
![]()
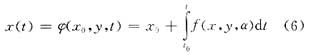

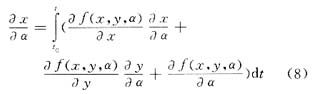
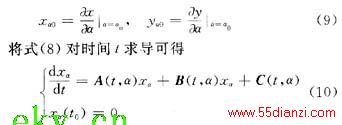
![]()

![]() 为惯性中心(center of inertia,简称COI)坐标框架[11]下发电机速度
为惯性中心(center of inertia,简称COI)坐标框架[11]下发电机速度![]() 转化为惯性中心坐标下的发电机速度
转化为惯性中心坐标下的发电机速度![]()
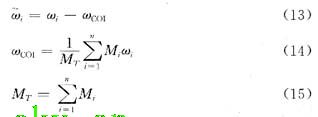
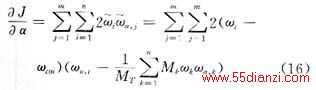
![]()


![]()
