高转速高精度机床主轴优化设计

     机械产品的设计, 一般需要经过提出课题、调查分析、技术设计、结构设计、绘画和编写设计说明书等环节。传统设计方法通常是在调查分析的基础上, 参照同类产品, 通过估算、经验类比或试验等方法来确定产品的初步设计方案。然后对产品的设计参数进行强度、刚度和稳定性等性能分析计算, 检查各项性能是否满足设计指标要求。如果不能满足要求, 则根据经验或直观判断对设计参数进行修改。
        整个传统设计过程是人工试凑和定性分析比较的过程, 因此, 这种方法只能是被动地重复分析产品的性能, 而不是主动地设计产品的参数。而优化设计是用数学规划理论和计算机自动选优技术来求解最优化的问题。对工程问题进行优化设计, 首先需要将工程设计问题转化为数学模型, 即用优化设计的数学表达式描述工程设计问题。然后, 按照数学模型的特点选择合适的优化方法和计算程序, 获得最优设计方案。

        1 优化设计及其数学模型
        优化作为一门学科与技术, 是一切科学与技术所追求的永恒的主题, 旨在从处理各种事物的一切可能的方案中, 寻求最优的方案。优化的原理与方法, 在科学的、工程的和社会的实际问题中的应用,
        这便是优化设计。机械优化设计则是优化设计在一切工程设计应用中的一个方面, 其本质是依据最优化的原理与方法, 且通常借助计算技术与计算机这一强有力的手段, 对某项机械设计, 在规定的各种设计限制条件下, 优选设计参数, 使某项或某几项设计指标获得最优值。它所追求的是最优结果、最佳设计等, 所遵循的是一套日益发展与完善的最优化理论与方法。所以, 整个设计过程是一个科学寻优的过程。
        用一组设计变量描述优化设计对象的设计内容、即描述优化意图和有关限制条件的数学表达式,称为优化设计的数学模型。它包含三个要素, 即设计变量、目标函数和约束条件。
        设计变量是用一组设计参数的最优组合来表示的。设计变量的个数就是优化问题的维数。有n 个设计变量x1, x2, !, xn 的优化问题, 其维数为n。由n个设计变量为坐标所组成的实空间称为设计空间。设计空间中, 点x 就代表一个设计方案(或称设计点), 以向量表示时, 可记为
        x = [ x1, x2,..., xn] T 或x∈ Rn          ( 1)
        式中Rn——代表n 维实空间。
        目标函数f ( x )是反映优化意向的关于设计变量的数学表达式, 可用来直接评价优化方案的好坏,所以又称为评价函数。为了规范化, 优化设计数学模型中通常规定求目标函数的极小值, 即
        minf( x )=f(x1, x2,..., xn )                ( 2)
        约束条件也称设计约束, 它是设计变量间或设计变量本身应该遵循的限制条件的数学表达式。约束条件按其表达式可分为不等式约束和等式约束两种, 即
        gj ( x ) ≤ 0( j= 1, 2, ..., m )   hv= 0( v= 1, 2, ..., p )                                                        ( 3)

        2  高转速、高精度数控车床主轴的优化设计
        主轴部件是机床的执行件, 它的功用是支承并带动工件或刀具, 完成表面成形运动, 同时还起到传递运动和扭矩、承受切削力和驱动力等载荷的作用。主轴部件的工作性能直接影响到机床的加工质量和生产率, 是机床中的一个关键部件。如图1所示为经过简化处理的高转速、高精度数控车床双支承主轴的力学模型。主轴支承采用角接触球轴承, 主轴的最高转速为8000r/min, 机床主轴的悬臂端受到的切削力F=20000N, 主轴内径d=40mm, 悬臂端许用挠度y0=0.05mm。要求主轴两支承跨度350mm≤ l≤ 600mm。外径70mm≤D≤ 150mm。悬臂端长度80mm≤a≤160 mm。主轴的材料采用40 C r。从机床主轴制造成本和加工精度的要求出发, 需要考虑主轴的自重和外伸段挠度这两个重要因素。选取主轴的重量最轻为设计目标, 将主轴的刚度作为约束条件。

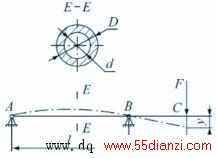
图1 主轴力学模型图

        2. 1 设计变量和目标函数
        主轴重量设计变量包括主轴的外径D (因主轴的外径在其长度内变化不大, D 取其外径平均值)、孔径d、两支承跨度l和外伸段长度a, 如图1所示。
        设计变量为
               

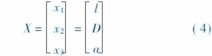
        机床主轴重量最轻优化设计的目标函数为
               

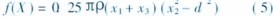
本文关键字：暂无联系方式机床，应用领域 - 机床