1.引言
在低压配电网中广泛采用了三相四线制系统。由于各种电能变换装置的应用以及中性线的存在,零序电流在中性线上相互叠加,会使得中性点偏移,三相电流不对称,也会导致中线电流大大超过它的额定值,造成中线故障;另一方面使得变压器过热,导致绝缘破坏,同时还会造成中线对地电势的提升。有源电力滤波器(Active Power FiLTEr,APF)因为能够根据不同的目的实现灵活的动态补偿且不容易和电网阻抗发生谐振,在三相四线制系统中已经得到了广泛的应用谐波及无功电流的检测和补偿电流的控制都是有源滤波器应用中的关键技术,检测算法中使用的低通滤波器又是影响检测精度与速率的关键因素。传统谐波检测多采取使用普通低通滤波器(LPF)的ip-iq 法,但是其计算量较大,稳态精度和动态性能不够理想。本文采用基于时域变换的谐波电流检测算法(Time-domain based Transform Algorithm,TTA)【1】,并将滑动平均值滤波技术应用到该算法中,可以有效地改善谐波检测的动、稳态性能。补偿电流的控制采用滞环比较法,该方法原理简单,响应速度快,且不含有特定频率谐波分量。
2.谐波及无功电流检测原理
将负载电流通过计算得到期望的基波正序有功电流,再与负载电流相减取反,即可得到谐波和无功电流。基于这种思想,目前谐波和无功的检测主要有以下几种方法【2】:
(1)采用模拟滤波器的谐波检测方法;
(2)基于傅立叶变换的谐波检测方法;
(3)基于小波分析的谐波检测方法;
(4)基于神经网络的谐波检测方法;
(5)基于瞬时无功功率理论的谐波检测方法;
(6)基于时域变换的谐波电流检测法。
2.1 基于时域变换的谐波及无功电流检测原理
在三相四线制系统中,常用的方法为基于瞬时无功功率理论的ip-iq 法,但是该方法需要多次的坐标转换,特别是在三相电流不平衡时计算量大大增加。本文采用的TTA 算法物理意义明确,适应范围广,对各种负载场合都能胜任,且可以很方便的应用于单相及多相系统。图1 所示为TTA 法谐波电流检测框图。
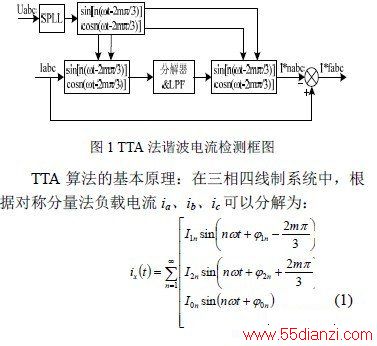

根据不同的补偿目的,分析如下:
①如果要补偿谐波、负序和零序电流可利用式(3)得到的各相基波正序电流分别与检测到的各相负载电流相减得到三相指令电流。如果在补偿谐波和不平衡电流的同时也补偿基波正序无功电流(全补偿),则可令式(3)中的Iq11=0 得到各相基波正序有功电流,再分别与检测到的各相负载电流相减得到三相指令电流。为了将流过电网中性线的电流控制为0,可将检测到的三相负载电流相加取反得到中线指令电流;
②如果只补偿第n 次谐波电流,则可将公式(1)
分别乘以2sin[n(ωt-2mπ/3)]、2cos[n(ωt-2mπ/3)]然后通过低通滤波器得到Ipxn、Iqxn,再利用式(4)得到各相第n 次谐波指令电流。中线指令电流要通过将三相补偿指令信号相加取反获得。
2.2 滑动平均值滤波器原理

在三相四线制系统中,大多数场合下偶次谐波电流含量较少,因此在下面的计算中将忽略偶次谐波电流。式(5)中,变换前任意次谐波电流in(t)中包含基波和3、5、7 等奇次谐波,变换后为直流分量(对应于基波)和2、4、6、8 等偶次谐波。设基波电流的周期为T,若对式(5)在T/2 时间内积分,那么偶次谐波成分的积分结果为零,保留下来的即为基波电流对应的直流分量。其计算式为:
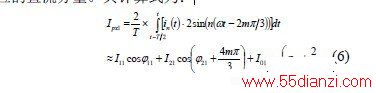
3.谐波检测及有源滤波器控制仿真
3.1 三相四线并联型有源滤波器仿真模型
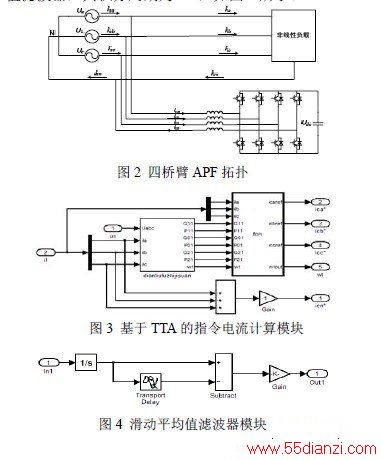
在三相四线制系统中常用的有源电力滤波器主电路结构为三桥臂电容分裂式结构和四桥臂结构【3】。三桥臂结构中线接在串联电容器中间,全部的中线电流都流经直流侧电容器,其数值较大,且可能出现电容电压不平衡问题,使控制变得复杂。四桥臂结构虽然多一组桥臂,成本有所增加,但是其直流侧控制比三桥臂结构要简单。本文所采取的主电路结构为四桥臂形式,如图2 所示。
利用Matlab 软件建立了三相四线制并联型电力有源滤波系统的仿真模型。图3 所示为基于TTA 算法的指令电流计算模块,其中其中的滤波器采用滑动平均值滤波器,其积分周期为T/2,如图4 所示。
3.2 谐波检测仿真及分析
由于谐波及无功电流的检测是影响APF滤波效果的关键,所以首先对传统的ip-iq法和TTA法检测谐波电流的效果进行了仿真对比。三相负载电流ilx 由Embedded MATLAB Function模块编程产生,分别包含基波、2次和5次谐波电流,如式7所示。
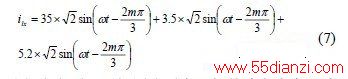
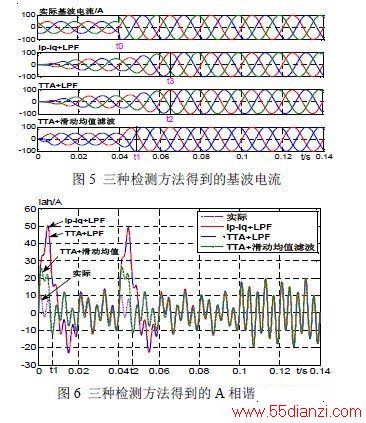
图5由上到下四幅图分别为三相基波电流实际波形、使用LPF的ip-iq法检测到的、使用LPF的TTA法检测到的及使用滑动平均值滤波的TTA法检测到的三相基波电流波形。其中LPF采用IIR型的Butterworth低通滤波器,2阶,截止频率为20Hz。在0.04s时(t0时刻)基波电流幅值突增,可以看出,使用滑动平均值滤波器的TTA法在t1时刻就能检测出正确的基波电流,用时不到半个基波周期,而在t2、t3时刻使用普通LPF的ip-iq法和TTA法才能检测出正确的基波电流,延时较长(超过一个基波周期)。图6所示为三种不同检测方法得到的A相谐波电流波形。在0.04秒时A相基波电流突增一倍,在0.1秒时5次谐波电流突增一倍。当基波电流发生突变后,使用了滑动平均值滤波的TTA法在t2时刻就能正确的检测出谐波电流,延时较小(不到10ms),具有良好的动、稳态性能;而另两种方法在0.06s时才能检测出正确的谐波电流,延时较为严重。当基波电流不变而谐波电流发生突变时,由于谐波电流是由检测到的总电流减去基波电流得到的,因此在这种情况下三种方法都能很快的检测出正确的谐波电流。
3.3 三相四线制APF 控制效果分析
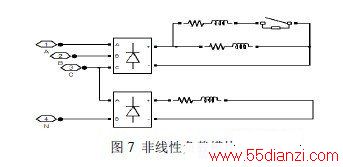
将带有滑动平均值滤波的TTA 检测法应用于三相四线制APF 系统中,为了检验其抑制谐波和不对称电流的能力,以及对中线电流的补偿效果,建立了三相四线制系统仿真模型。模型主电路采用四桥臂结构,补偿电流输出采用滞环控制(环宽2H=0.2)。负载采用三相不控整流器,并在C 相和中性线之间接入单相不控整流器造成三相之间不对称。不控整流器所带负载均为阻感负载,如图7 所示。在三相不控整流的负载侧并联阻感负载,并加入Breaker 开关以模拟负载突变。一些重要仿真参数列举如下:

仿真时采用全补偿方式,在0.04 秒时APF 投入控制,在0.1 秒时,三相不控整流器的负载加重一倍将负载电流ila乘以2sin(ωt)后所得电流分别使用IIR型的Butterworth 低通滤波器和滑动平均值滤波器进行滤波,所得波形如图8 所示。由图8 可知,无论从动态响应时间还是滤波效果上看,采用滑动平均值滤波器都优于采用普通低通滤波器。电源侧A、B、C 三相和中线电流如图9 所示。由于中线指令电流由三相负载电流直接相加取反得到,运算速度快,所以在APF 投入的瞬间,系统中线电流就得到了很好的抑制;其他三相指令电流需要经过一系列计算得到,因此有一定的延时,但延时较小,谐波补偿效果较好。
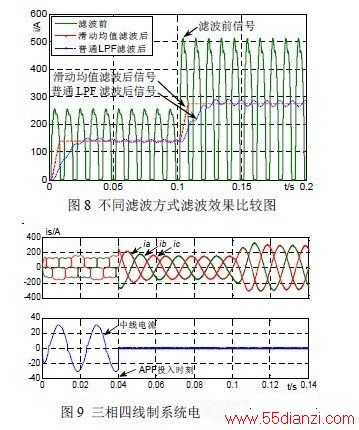
表1 为A 相补偿前与补偿后的主要次谐波电流含有率HRIn(%)。从表中可以看出5、7、11 等主要次谐波得到了很好的补偿。总的电流谐波畸变率也由滤波前的27.89%变为了滤波后的2.84%。


本文关键字:滤波器 滤波-陷波电路,单元电路 - 滤波-陷波电路