埋嵌式元件共面度测量方法研究

　　下文以构造点A1、B1、D1对应的平面α1为例，介绍使用PCB板面测量点的坐标、采用点法式方法构造基准平面的过程：

　　（1）选取构造点：设A1点坐标为（x1,y1,z1），B1点坐标为（x2,y2,z2），D1点坐标为（x4,y4,z4）；

　　（2）构造向量：向量A1D1记为a1{（x4-x1），（y4-y1），（z4-z1）},向量A1B1记为b1{（x2-x1），（y2-y1），（z2z1）};

　　（3）计算平面法向量：

　　（4）构造平面α1:点法式方程为：

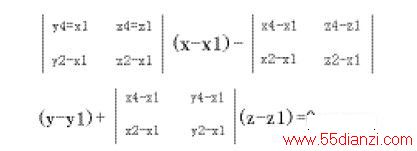
　　同理可利用A1、B1、C1点构造B1点对应的基准平面α2,B1、C1、D1点构造C1点对应的基准平面α3,C1、D1、A1点构造D1点对应的基准平面α4.

　　4.2.2 测量数据量

　　为兼顾测量效率和测量结果准确性，设计每个点测量1、2、3次的计算方法，其中每个点测量2、3次时，每次测量时需对同一位置测量2、3次，计算共面度时各点坐标取测量的平均值。

　　计算共面度时的优先顺序为：单点3次>单点2次>单点1次。可在优先（Excel）表格内编程，实现数据优先级设定。

　　4.2.3 共面度值计算

　　如图10,计算铜块表面A（xA,yA,zA）点到基准面的共面度，基准面为点A1、B1、D1所构造的平面α1,已知A1点坐标为（x1,y1,z1），平面α1的点法式方程为：

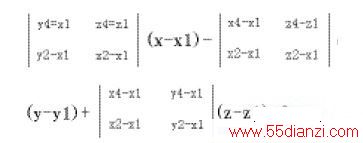
　　则A（xA,yA,zA）点到其基准平面α1的距离dA可用下式计算：

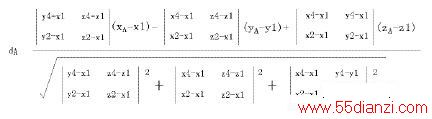
　　同理，可计算铜块表面其它各点B、C、D距离其对应的基准平面的距离dB、dC、dD.对于铜块表面中央点E,由于其距离PCB表面参考点A1、B1、C1、D1均较远，故分别计算其到α1、α2、α3、α4四个基准平面的距离dE1、dE2、dE3、dE4,并考量四个计算值的差异，用以辅助评价被测PCB样品是否存在翘曲、样品在测量台面上是否被水平放置。

　上述铜块上各点到基准平面的距离dA、dB、dC、dD、dE1、dE2、dE3、dE4,即为被测铜块表面各点的共面度值。dA、dB、dC、dD、dE1、dE2、dE3、dE4中绝对值最大者，即为被测铜块的共面度值。

上一页  [1] [2] [3] [4] [5]  下一页

本文关键字：测量  传感-检测-采集技术，电子知识资料 - 传感-检测-采集技术