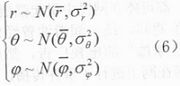3 数据融合算法
基于最大似然估计准则的估计器是一种基本估计器。若未知矢量x(既可是确定的,也可是随机的)与观测值有如下关系:
z=g(x)+r (5)
则可用最大似然估计求出该矢量x。式中,r是一个与x无关,且具有已知概率密度函数fr(r)的随机矢量。最大似然估计准则选择出最可能的观测值z的,即fz|x(z|x)为最大的估计

。不管x的概率是什么,只要知道了观测误差的概率分布就可求出该估计。
对本文讨论的情况,对于同一个x存在一组探测{zi},使f{z}|x({z}|x)取得最大值的就是最大似然估计。已知任意两次探测相互独立,各探测分量(r,θ,φ等)也相互独立,且服从正态分布,即有:
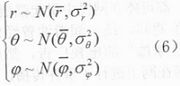
根据此条件可以求出f{z}|x({z}|x)和grad(Inf{z}|x)。再用梯度下降法即可求出使ln f{z}({Z})取得最大值的就是目标位置的最大似然估计值。
若上述测量集合{Zi}只包含一个两坐标探测器(两坐标雷达或红外探测器)点迹,则采用梯度下降法只能收敛到弧线段或直线段上,而无法收敛到一点。因此上面的估计只针对测量集合{Zi}至少包含两个探测器或包含三坐标雷达的探测系统的情况。
4 应用
在某项目研制中,应用本文所讨论的融合算法,三坐标雷达探得的目标和至少两个探测器同时探测得到的目标都能形成完整的三维融合点迹。而仅被一部两坐标探测器探测到目标的点迹集合无法通过前面的方法变成三维点迹。处理后的整个点迹序列表现为三维融合点迹和原始的二维点迹分段交替出现。为了得到最终的融合航迹,需选用一组恰当的卡尔曼滤波器组进行切换滤波。即当存在三维点迹时用探测值形式为(x,y,z)的卡尔曼滤波器进行滤波,当遇到无三维点迹时切换为两坐标探测器进行卡尔曼滤波,并且切换时沿用前一滤波器估计出的状态
向量和状态向量误差协方差作为滤波器的起始条件,由此就成功地融合出了完整的三维航迹,同时能很好地估计出目标速度和加速度。
5 结语
本文提出的多制式传感器数据融合算法能有效地解决多制式传感器系统中的数据融合问题;算法简单,易于工程实现。
上一页 [1] [2]
本文关键字:传感器 传感-检测-采集技术,电子知识资料 - 传感-检测-采集技术