数字滤波在数字信号处理中占有重要的地位, 数字滤波器又分为无限冲激响应滤波器(IIR)和有限冲激响应滤波器(FIR)。 FIR滤波器具有不含反馈环路、结构简单以及可以实现的严格线性相位等优点,因而在对相位要求比较严格的条件下,易采用FIR 数字滤波器。同时,由于在许多场合下,需要对信号进行实时处理,因而对于单片机的性能要求也越来越高,普通的单片机例如MCS51难以满足这一要求。由于DSP控制器具有许多独特的结构,例如采用多组总线结构实现并行处理,独立的累加器和乘法器以及丰富的寻址方式,采用DSP控制器就可以提高数字信号处理运算的能力,可以对数字信号做到实时处理。本文根据FIR数字滤波器的基本原理在TMS320F240中实现了FIR实时数字滤波。
1基本原理
一个截止频率为ωc(rad/s)[1]的理想数字低通滤波器,其表达式是:
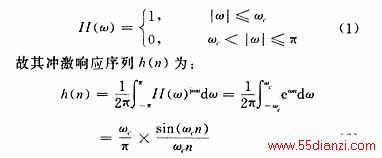
这个滤波器在物理上是不可实现的,因为冲激响应具有无限性和因果性。为了产生有限长度的冲激响应函数过截短保留冲激响应,可以加窗函数将其截短,通过截短保留冲激响应的中心部分,就可以获得一个线性相位的FIR滤波器。例如,使用一个简单的矩形窗设计一个长度N=127,截止频率ωc=π/2的低通滤波器,冲激响应h(n)可表示为:

一般来说,FIR数字滤波器输出y(n)的Z变换形式Y(z)与输入x(n)的Z变换形式之间的关系如下:
![]()
实现结构如图1所示。

从上面的Z变换和结构图可以很容易得出FIR滤波器的差分方程表示形式。对式(4)进行反Z变换,可得:
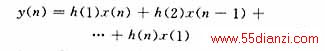
式(5)为FIR数字滤波器的时域表示方法,其中x(n)是在时间n的滤波器的输入抽样值。根据式(5)即可对滤波器进行设计。
在实际的FIR滤波器的设计中,一般采用计算机辅助设计。Matlab是一套功能强大的适应于科学工程计算的可视化高性能语言,他提供了2种窗函数方法设计FIR滤波器:一种是标准通带滤波器的设计FIR1;一种是多带FIR滤波器的设计FIR2。函数FIR1只能设计标准的低通、高通、带通和带阻线性相位FIR滤波器。函数FIR2也设计加窗的FIR滤波器,但他针对任意形状的分段线性频率相应,这一点在FIR1中是受到限制的。这里用FIR1设计一个截止频率为ωc的N阶低通滤波器,设计如下[2]:
H=FIR1(N,ωc)
其中:N为FIR滤波器的阶次,ωc为归一化后低通滤波器的截止频率(即Nequist频率=1)。
为了提高滤波的精度,在将H参数固化到EPROM前,应对其进行归一化处理,即为Q15的格式(最高位为符号,其余为小数)。
2FIR滤波器DSP的实现
滤波前首先要读取A/D转换值, TMS320F240的片内外设中含有模数转换模块,他包括2个独立的A/D转换器,其A/D转换的值可以直接通过读取FIFO结果寄存器得到,指令如下:
LACL ADCFIFO
将读取的结果存放到数据存储器中。由于H参数是固化在EPROM中,滤波前要将H参数从程序存储器读到数据存储器中。图2说明了如何寻址实现FIR滤波器。

由式(5)可知,输出y(n)是单位脉冲响应h(n)和输入信号的采样值x(n)的卷积和。在TMS320F240的指令中,MPYA在一个机器周期内能够完成乘积和累加的功能,利用T寄存器和辅助寄存器AR1,AR2和AR3即可实现式(5)中的卷积和。其中AR1存放H参数的开始地址,AR2存放采样值的开始地址,AR3存放滤波的阶次。实现式(5)的汇编语言如下:

FIR数字滤波器总程序流程图如图3所示。
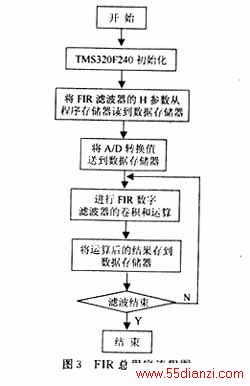
3结语
随着信息技术的深入和计算机技术的飞速发展,数字信号处理技术已经发展成为一门关键的技术学科。而数字滤波作为数字信号处理的一个基本的学科分支,也得到了越来越广泛地应用。本文介绍了由TMS320F240实现的数字滤波器,通过在电力谐波监测仪中的应用,我们发现在滤波阶数不很高的情况下(例如64阶),该滤波器实时滤波效果比较理想,并且他可以随时调整滤波器参数,具有比较高的实用价值。
本文关键字:滤波器 综合-其它,单片机-工控设备 - 综合-其它
上一篇:基于DSP的流星信道模拟器设计