麦道90机载变速恒频发电系统的谐波分析

图3三相半桥式逆变器的输出电压波形

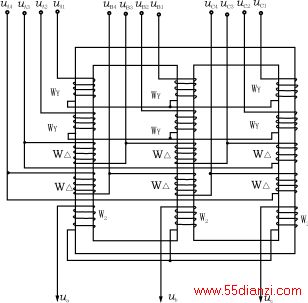
图4三相变压器的结构示意图

1.19003a－1.37412=0

a=1.37412/1.19003=1.1546936

即当a=1.1546936时，就可以消除2KN±5组谐波，也即消除5.7.17.19.29.31.41.43.53.55…次谐波。此时的波形如图示2（b）所示。

　　将a=1.1546936代入方程式（1）即可得到基波与各次谐波幅值的方程式的：将n=1.3.5.7…代入上式，即可算出基波与各次谐波的幅值。

其中基波幅值等于同样用谐波幅值与基波幅值之比UAm(n)/UAm(1)来表示阶梯波中各次谐波的含量时，可以把n=1.3.5.7…代入方程式（4），即可算出a=1.1546936时各次谐波的含量如表中a=1.1546936一栏中的UAm(n)/UAm(1)数值所示。

对比表达式中a=1和a=1.1546936时的谐波含量可知：

　　（1）无论是a=1还是a=1.1546936，都能消除零序谐波，这时因为零序谐波的消除与a的取值无关，而是与叠加和接线方式有关。

　　（2）当a=1.1546936时，可以使正序与逆序谐波中的5.7.17.19.29.31.41.43.53…次谐波被消除，进一步减少了阶梯波中的谐波含量。

　　（3)当a=1.1546936时，11、13、23、25、35、37、47、49…次谐波，保持a=1时的谐波含量不变。

　　这就说明：a=1.1546936比a=1可以减少更多的谐波含量。所以a=1.1546936比a=1具有更好的消除谐波效果。因此阶梯波的阶差相对值取：1.1546936、1、1、1.1546936/2、1.1546936/2比取1、1、1、1/2、1/2要好的多。这就是我建议改进的原因。

3结论

　　（1）比例系数a取1.1546936比a取1具有更好的消除谐波效果，它可以使正序和逆序谐波中的5、7、17、19、29、31、41、43、53…次谐波完全被消除，进一步减少了谐波含量，特别是消除了5、7次低次谐波更具实用意义。对于11、13、23、25、35、37、47、49…次谐波，则保持与a=1时的谐波含量不变。这就是说a=1.1546936比a=1可以减少更多的谐波含量。

表1

MD90所用方案a=1建议改进方案a=1546936nUAm(n)/UAm(1)UAm(n)/UAm(1)11.0000011.00000303050.011495070.00630709090110.01197110.01197130.01013130.01013150150170.00259170190.00302190210210230.04348230.04348250.04000250.04000270270290.00198290310.00142310330330350.00376350.00376370.00356370.00356390390410.00108410430.00103430450450470.02128470.02128490.02041490.02041510510530.00108530550.00080550

　　（2）将a=1改成a=1.1546936只需把输出接成“Y”形的逆变器所联接的变压器初级绕组，由WY=W△/1.5改成为WY=W△/1.7320404即可。

　　（3）零序谐波的消除与a的取值无关，只取决于叠加和接线方式。

　　（4）MD90VSCF输出变压器是三相变压器，其结构如图4所示，每一铁芯柱上有五个绕组，即四个初级绕组和一个次级绕组，当a=1时WY=W△/1.5，当a=1.1546936时WY=W△/1.7320404。

参与文献

1朱普安等．机械变速恒频（VSCF）交流电源的谐波分析．电力电子技术，1999No.4

2BiringerP.PDeterminationofHarmonicsofConverterCurrentand/orVoltagewaveforms(NewmethodforForuiercoefficientcalculations.PartI:FouriercoefficientsofHomogeneousFunctions)。

3刘凤君．可控硅逆变器，人民邮电出版社，1987

上一页  [1] [2] 

本文关键字：谐波  电工文摘，电工技术 - 电工文摘