电力系统实时等值及电压稳定性分析
邱晓燕,李兴源,王建, 刘红超
(四川大学电气信息学院, 四川省 成都市 610065)
摘 要:根据实时测量的负荷节点的电压、电流相量,将整个系统等值为一简单的两节点系统,在此基础上进行电压稳定性分析,提出了一种根据定义的节点电压稳定性指标能快速估计节点电压稳定性的方法,并将其扩展到计及负荷静态特性的情况。文章分析了发电机无功功率极限对电压稳定性的影响。通过中国电力科学研究院EPRI-36节点系统算例,验证了该分析方法是一种简单、快速、有效的方法,且可应用于电力系统电压稳定性的实时监控。
关键词:实时等值;电压稳定性;负荷静态特性;无功功率极限;电力系统
POWER SYSTEM EQUIVALENT IN REAL TIME AND
VOLTAGE STABILITY ANALYSIS
QIU Xiao-yan,LI Xing-yuan,WANG Jian,LIU Hong-chao
(School of Electrical Engineering and Information,Sichuan University,
Chengdu 610065,Sichuan Province,China)
ABSTRACT: According to the voltage and current phasors at the load bus which is measured in real-time, the whole system can be equivalent to a simple 2-bus system and on this basis the voltage stability analysis is carried out and a method by which the stability of nodal voltage can be quickly estimated with the defined nodal voltage index is presented and is expanded to the situation taking account of the static characteristics of loads. Here, the influence of reactive power limits on voltage stability is analyzed. By means of the calculation example of CEPRI-36-bus system the verification result shows that the presented method is simple, fast and effective and can be used to the real-time supervision and control of power system voltage stability.
KEY WORDS: Real-time equivalent;Voltage stability;Load static characteristics;Reactive power limits;Power system
1 引言
随着电力工业的发展和电力体制的改革,现代电力系统经常运行在稳定极限附近,因而电压稳定性问题较为突出。目前很多学者对其进行了研究,提出了判断电压稳定性的各种指标和计算电压稳定裕度的算法[1-3]。由于电力系统规模庞大, 电压稳定性的研究总是在等值的基础上进行的[3]。随着实时同步测量技术的发展,已可以从安装于系统母线上的相量测量装置直接测得母线的电压相量和注入母线的电流相量[4]。因此,现在人们越来越注重于根据实时的直接测量参数进行等值,并估计对电压稳定极限的逼近程度,提出了用基于相量测量的算法来确定离电压崩溃点的距离[5,6]。
本文提出根据实时测得的负荷电压和电流相量,从负荷节点看进去,将整个系统等值为两节点系统,然后根据两节点系统的电压稳定性条件,定义一电压稳定性指标,再根据此指标值快速地判断该节点的电压稳定性的方法,并将这种方法扩展到计及负荷静态特性的一般情况。文中还分析了发电机无功功率极限对系统电压稳定性的影响。最后给出了中国电力科学研究院EPRI–36节点系统的算例分析。
2 基于实时相量测量的电力系统等值
对于任一时刻k ,从某一负荷节点看进去,可以将整个系统等值为两节点系统,即所要研究的负荷节点和其余外部系统等值得到的电源节点的系统,如图1所示。图中,PLK+jQL,k 为时刻k的负荷功率,此时刻的电压为Vk ,电流为Ik ,外部等值系统的电势为Ek ,阻抗为Zk 。
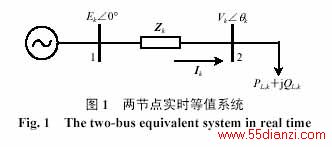
随着系统运行状态的变化,图1中外部等值系统的电势和阻抗都将发生变化。本文根据负荷母线电压、电流相量的测量值,实时估计外部等值系统的电势和阻抗。由图1可得
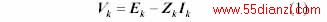
将外部等值系统电势和阻抗,以及负荷节点
显然,要估计时刻k的电势和阻抗,仅用同一时刻的电压、电流相量测量值是无法实现的,至少应有两个时刻的电压、电流相量的测量值才能实现。本文采用递推最小二乘法进行估计,其递推公式为
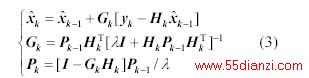
式中 λ 为遗忘因子;I 为单位矩阵;Pk 为时刻k估计值的方差阵;Gk 为时刻k的增益系数矩阵。
3 两节点等值系统电压稳定性条件
当负荷用恒功率表示时,电压不稳定点与最大功率传输点相一致,此时等值电压源电势Ek 与负荷节点电压Vk 的关系为
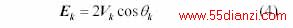
式(4)表明,在最大功率情况下,等值阻抗Zk 上的电压降ΔVk 等于负荷节点的电压Vk ,即 
很明显,当Ivk=1 时,该节点的电压达到稳定极限。因此可将时刻k所有负荷节点电压稳定性指标Ivk 中的最小值作为衡量整个系统电压稳定性的指标,即
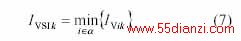
式中 α 为负荷节点集合;i为任一负荷节点。
指标Ivk 不仅可以用来估计负荷节点的电压稳定性,比较每一个负荷节点的Ivk 值,而且还可以据此找到采取控制措施最有效的位置。一般说来, 值越小的节点越容易失去电压稳定性,因此在 值较小的负荷节点上采取控制措施,对于整个系统的电压恢复会收到较好的效果。
4 计及负荷静态特性时的电压稳定性指标
负荷特性对电压稳定性的影响非常大,当计及负荷的电压静特性时,电压稳定极限将超过最大传输功率极限。
计及电压静特性的负荷(ZIP)模型为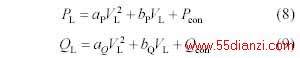
式中 系数a、b分别表示恒阻抗、恒电流负荷所占的比例;Pcon 、Qcon 表示恒功率负荷分量;VL 表示负荷节点电压。
计及负荷电压静特性后,在上述假设负荷为恒功率条件下推导得到的电压稳定性条件需要进一步推广到一般情况。
图2为计及ZIP负荷的两节点系统等值。 图中,E=E∠0° ,V=V∠θ ,ZL 、IL 分别表示 恒阻抗、恒电流负荷分量,其参数由式(8)、(9)获得。图2(b)为从恒功率负荷分量Pcon+jQcon 看进去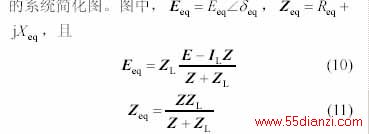
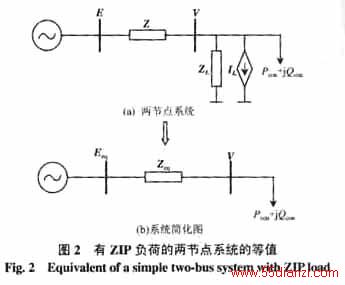
图2(b) 的结构与图1相同,因此可用Eeq 代替E ,用θ-δeq 代替 ,则得
上式中ΔVeq 即为等值阻抗Zeq 上的电压降。 因此,将式(6)推广可得到计及负荷电压静特性(ZIP)时的电压稳定性指标为
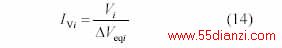
同理,当Ivi=1 时,该节点电压即为电压稳定的极限值。
5 算例分析
本文采用中国电力科学研究院EPRI–36节点系统作为算例进行分析。该系统共有9个负荷节点,其编号分别为9、16、18、19、20、21、22、23、29。
表1中列出了所有负荷均为恒功率模型时,临界状态下各负荷节点的电压稳定性指标值。从表中可以看出,临界状态下,各负荷节点的电压稳定性指标非常接近于1,从而验证了式(6)所定义的指标是可行的。从表中还可以看出,节点16和29的IV值相对较低,这说明在这两节点处最容易发生电压崩溃。

下面以节点29为例进一步分析负荷静态特性对电压稳定性或电压稳定性指标的影响。分析中只计及负荷节点29的电压静特性(其中恒阻抗负荷占15%,恒电流占10%,恒功率占75%),其余负荷仍为恒功率模型。在临界状态下,节点29的IV值为1.0050,非常接近于1,这说明式(14)的正确性。
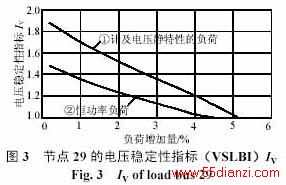
图3给出了节点29的电压稳定性指标IV随着负荷增加时的变化情况。实际上,其它负荷节点的电压稳定性指标也有相同的变化趋势,即随着负荷的增加,IV的值逐渐减小,当到达临界状态时,其值接近于1。此曲线是比较平滑的。从图3可以看出,计及负荷的电压静特性之后,系统的电压稳定性裕度有所增加,因此,按恒功率负荷估计的电压稳定性裕度对于含有各种类型负荷的综合负荷来说是比较保守的、不精确的。
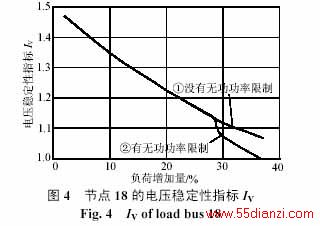
下面通过算例说明发电机无功功率极限对电压稳定性的影响。发电机节点5的无功功率极限为5Mvar。经过分析,当发电机的无功功率达到极限时,负荷节点18处最容易发生电压崩溃。图4为节点18的IV变化曲线。其中,曲线①为没有无功功率限制时的曲线,其变化比较平滑,曲线②为有无功功率限制时的曲线,在发电机节点5达到无功功率极限时出现一很陡的下降,即IV的变化在此点出现不连续。因此,实际应用电压稳定性指标IV时,必须实时监控发电机的无功储备,密切注意当发电机达到无功功率极限时IV产生突降后是否小于等于1。
6 结论
本文根据实时等值的两节点系统所提出的电压稳定性指标IV,可以快速估计节点电压的稳定程度,并且适合于计及负荷电压静特性的情况。当达到发电机无功功率极限时,电压稳定性指标将出现骤降现象,因此,实用中可以根据系统的实际情况,设定一阈值,当电压稳定性指标低于此值时,即认为系统将发生电压崩溃,应立即启动相应的保护措施。这种方法简单、快速,可应用于电力系统电压稳定性的实时监控。
参考文献
[1] Ajjarapu V,Lee B.Bibliography on voltage stability[J].IEEE Trans on Power Systems,1998,13(1):115-125.
[2] Taylor C W.Power systems voltage stability[M].New York: McGraw-Hill,Inc,1994.
[3] 李兴源,王秀英(Li Xingyuan,Wang Xiuying).基于静态等值和奇异值分解的快速电压稳定性分析方法(Fast voltage stability analysis methods based on static equivalence and singular value resolution)[J].中国电机工程学报(Proceedings of the CSEE),2003,23(4):1-4.
[4] Phadke A G.Synchronized phasor measurements in power systems[J].IEEE Trans on Computer Applications in Power,1993,6(2):10-15.
[5] Vu K,Begovic M M,Novosel D et al.Use of local measurements to estimate voltage-stability margin[J].IEEE Trans on Power Systems,1999,14(3):1029-1035.
[6] Borka Milǒsević,Mirǒslav Begović.Voltage-stability protection and control using a wide-area network of phasor measurements[J].IEEE Trans on Power Systems,2003,18(1):121-127.
本文关键字:稳定性 电工文摘,电工技术 - 电工文摘