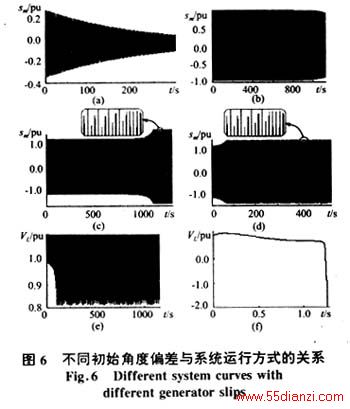
当sm，0在0～1．302 447 9之间变动时，系统经过初始的暂态振荡后，收敛到由静态方程决定的平衡点，但在sm，0不断变大的过程中，系统收敛的速度越来越慢（如图6（a）和6（b）所示）；在sm，0≈1．3024479时，系统在经历长时间暂态过程后，最终收敛到一个稳定的混沌吸引子上（见图6（c）相轨迹不规则的振荡和图7中它的Piocaré映射）。需要指出的是，当sm，0在1．3024478～1．302447 9（两者仅相差10－7）变动时，系统并未出现图5所示的逐级分岔现象（即未发现2、4等偶数倍周期），而是直接由收敛到平衡点跃变成收敛到混沌吸引子；同样，另一次跃变发生在1．698 037 8～1．698 037 9之间，当sm，0＝1．698 037 8，系统的终态受奇异吸引子控制（见图6（e）的轨迹和图9的Piocaré映射），而当sm，0仅增大10－7后，系统变为迅速的单调失稳模式（见图6（f）中的轨迹）。在上述系统参数不断变化过程中，系统行为出现跳跃变化的点，对应着系统方程的动态分岔现象［6］。
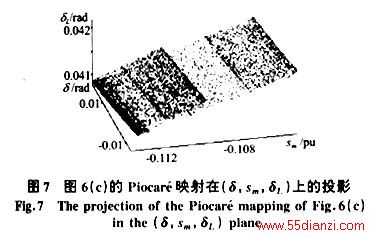
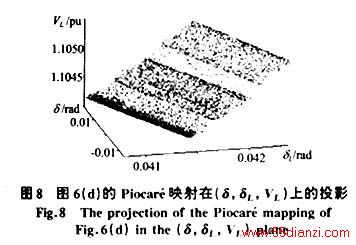
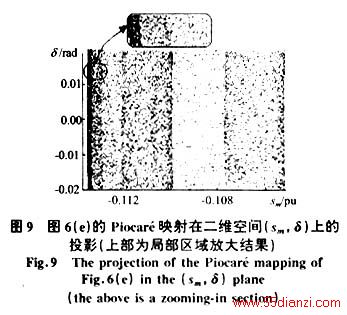
由图7－9可知，系统各Piocaré映射精细结构明显且很相似，都是由相互间隔，密度不均的线条构成，对各映射点的出现次序（点序）研究可知，在Piocaré截面上点的出现次序没有规律，表明系统映射不存在任何稳定的收敛点。点序无规律，点的空间分布有精细结构，是混沌现象Piocaré映射的鲜明特征。
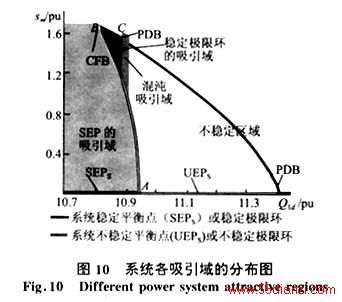
将上述过程中能够收敛到稳定的混沌吸引子的区域定义为混沌吸引域；能够收敛到系统稳定平衡点（SEP）的区域定义为SEP的吸引域［7］；以及能够收敛到稳定（单周期或多周期）极限环的区域定义为极限环的吸引域，3块区域示于图10（其他阴影部分为不稳定区域）。图中系统的静态平衡点（图中SEPs指稳定平衡点集和UEPs指不稳定平衡点集）对应于图中的横轴。在A点处系统发生Hopf分岔，由A点开始的翼状曲线
是Hopf分支在Q1 d－sm平面上的投影；在B点处Hopf分支发生了鞍节点分岔，称为CFB［4］（Cyclic－Fold－Bifurcation），不稳定的Hopf分支变为稳定的Hopf分支；在C点处系统发生第一次倍周期分岔PDB（Period Doubling Bifurcation），在其右端不远处即出现上述定义的混沌吸引域。
2．4 不同的导致途径与系统扰动的关系
由上分析可知，本节所给的两种导致混沌现象出现的途径有本质的区别。
由2．2节仿真计算可以看出，最终的混沌行为可能起始于一个系统的（不稳定）平衡点。因而途径一的存在，预示着电力系统在经受小的扰动时，其扰动后的行为也可能是混沌的。但从途径一的演变过程可以看出，在系统出现混沌行为之前，必然首先出 现单周期轨迹，从而表明系统中已有稳定的极限环，当系统轨迹由收敛到一个稳定平衡点变为收敛到一个稳定的极限环，说明Hopf分岔已经发生。因而在小扰动稳定域的研究中，其域边界的组成，不必包含混沌约束边界［8］。
第二种导致混沌行为的途径昭示：经历大扰动后的系统行为可能是混沌的。由2．3节仿真过程可知，在系统轨迹收敛到稳定平衡点和收敛到混沌行为以及最终单调发散三者之间，系统并未出现稳定的极限环（可能存在不稳定极限环）。因而在系统经历激烈扰动后，事故后行为，完全有可能是混沌的。
图10所示的各吸引域的分布情况，给人们提供了关于电力系统模型的一个更为整体的认识，但是从物理上看，即使在大扰动的情况下，sm的取值也不可能太大（最大约为0．3），因而工程实际中关心不到图10上部的区域。
3 结论
本文主要深入研究了电力系统中可能导致混沌现象出现的两种途径和其内在的规律，以及其与电力系统扰动和稳定性之间的关系。同时，利用Piocaré截面技术，第一次完整地给出了电力系统中混沌行为的整体分岔图和Piocaré映射图，并详细分析了其中的精细结构和演变过程。
参考文献：
［1］ Ajjarapu V，Lee B．Bifurcation theory and its application to
nonlinear dynamical phenomena in an electrical power system ［J］．IEEE－PWRS，1992，7（1）：424－431．
［2］ Chiang HD，Liu CC，etal．Chaosin asimple powersystem［J］．IEEE－PWRS，1993，8（4）：1407－1417．
［3］ Hua O W，Eyad H A，et al．Bifurcations，chaos，and crises involtagecollapse of a model power system［J］．IEEETrans onCircuitsand Systems－I：Fundamental Theory and Applications，1994，41（3）：294－302．
［4］ Tan C W，Varghese M，Varaiya P，etal．Bifurcation，chaos，andvoltage collapsein powersystems［J］．ProceedingsoftheIEEE，1995，33（11）：1484－1495．
［5］ Rajesh K G，Padiyar K R．Bifurcation analysis of a three nodepower system with detailed models［J］．Electrical Power and Energy Systems，1999，21（5）：375－392．
［6］ Thompson JM T，Stewart H B．Nonlinear dynamic and chaos［R］．John Wiley＆Sons Ltd．1986．
［7］ 余贻鑫，王成山（Yu Yixin，Wang Chengshan）．电力系统稳定性的理论与方法（Theory and method of powersystemstability）［M］．北京：科学出版社（Beijing：Science Press），1999．
［8］ Yu Yixin，Jia Hongjie，Wang Chengshan．Chaotic phenomena and
smallsignal stability region of electrical power systems［J］．Science in China(Series E),2001,44(2):187-199
本文关键字：暂无联系方式电工文摘，电工技术 - 电工文摘
