基于人工神经元网络的电力系统谐波测量方

　　　(9)
　　神经元的学习采用最小均方(LMS)算法，用
e(t)来调节连接权值w。其公式为
　　w_i(t＋1)＝w_i＋ηe(t)x_i(t)＋α［w_i(t)－w_i(t－1)］　　(10)
　　θ(t＋1)＝θ(t)＋ηe(t)＋α［θ(t)－θ(t－1)］　　　(11)
式中　η为学习率，0<η≤1，η取值太大会影响稳定性，太小又会使收敛速度过慢；最后一项为惯性项，加上它可以使η取值大一些，以加快学习收敛速度，0<α≤1。
　　 经过若干次迭代，E［e²(t)］逐渐趋向于最小值，权值逼近最佳值，因而ANN自适应谐波检测电路可实现谐波电流的动态检测。学习算法的第i支路见图3。

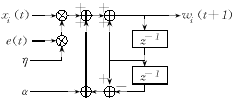
图3　学习算法的第i支路电路图
Fig.3　Learning algorithm circuit of No.i branch

4　动态检测的二级ANN自适应滤波
　　为满足动态检测的需要，应进一步提高收敛速度并保证ANN稳定，则假设

v(t)＝w(t)－w_opt(12)

式中　v(t)为权值的畸变量；w_opt为权值最佳值。
　　随η值的增加，权值畸变量v(t)加大，导致神经元网络输出畸变，甚至使ANN输出不稳定；同时，最小均方误差ζmin较大也会使权值畸变较大。
　　本文仅以基波的自适应滤波为例进行分析。
　　在理想情况下，w＝w_opt,w_1s sinωt＝i_1p，w_1c cosωt＝i_1q，若权值畸变量v(t)不为零，即w_1s sinωt＝i_1p＋i_dp，w_1c cosωt＝i_1q＋i_dq，其中i_dp和i_dq分别为ANN检测基波正弦、余弦的畸变电流。i_dp和i_dq与i_1p和i_1q不相关，应用自适应噪声对消原理，添加二级ANN自适应滤波器，可滤除i_dp和i_dq,使输出电流i^*′₁的波形失真较小。因此实现了因提高收敛速度而加大一级ANN学习率η所引起的畸变减小，其结构如图4所示。同理，3、5、7、9、11次谐波对应的自适应滤波器亦应添加二级ANN，可提高收敛速度，又改善了检测效果。

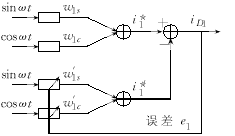
图4　二级自适应滤波基波支路
Fig.4　Two-level adaptive filter fundamental branch

5　仿真研究
　　在仿真研究中，参考输入的基波频率取ω＝2πf，f＝50 Hz；采样频率为f_s＝600f；流过非线性负载的电流为一方波，其周期为0.02 s、幅度为1 A。由于一定的采样频率对于基波，3、5、7、9、11次谐波及神经元阀值的影响是不同的，因而它们的权值学习率η和惯性系数α选取也不同，见表1。

表1　权值学习率η、惯性系数α和阀值
Tab.1　Step length η,inertial factor α and values

　基波3次5次7次9次11次阀值 η0.0160.0160.0120.0070.0050.0050.012 α0.030.020.010.010.010.010.01
　　方波的1、3、5、7、9、11次谐波和测量波形见图5(图中虚线为理论值波形)。仿真表明，在一个工频周期内该二级ANN的各输出值逼近于它们的理论值，当至收敛后它们之间就几乎没有幅度和相位的误差，而且初始权值的选取对收敛影响较小，可见系统的自适应能力较强。

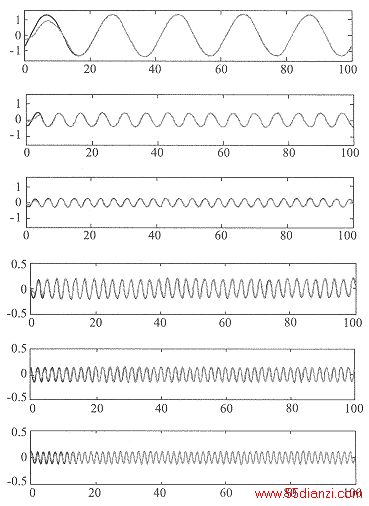
图中虚线为理论值波形，实线为仿真实测波形
图5　谐波电流测量波形
Fig.5　Measuring waves of harmonic currents

　　在一个工频周期末(20 ms)时刻的谐波测量值列于表2。其中1、3、5次谐波的幅度的相对误差在1%以内，相位的相对误差在2%以内；更高阶次谐波因含量太小，测量的相对误差有所增加，但稍后不到半个工频周期，其测量值即达到1、3、5次的测量精度，见图5。以上仿真分析表明，二级ANN自适应谐波测量精度较高、实时性良好。

表2　一个工频周期末(20 ms)时刻的谐波电流测量值
Tab.2　Measuring values of harmonic currents at 20 ms

次数电流幅值电流相位 理论值
/(p.u.)测量值
/(p.u.)绝对误差
/(p.u.)相对误差
/%理论值
/(p.u.)测量值
/(p.u.)绝对误差
/(p.u.)相对误差
/% 11.27321.2704－0.0028－0.22－30.00－29.490.51－1.70 30.42440.4218－0.0026－0.61－90.00－88.800.20－0.22 50.25420.2530－0.0012－0.47－150.00－148.72－1.280.85 70.18190.18450.00263.41－210.00－208.951.05－0.53 90.14150.14730.00584.10－270.00－267.732.270.84 110.11570.11800.00231.99－330.00－324.315.691.72
6　结论
　　本文根据信号处理中的自适应噪声对消技术和单个神经元的基本特点，结合谐波电流动态监测的要求，设计了二级ANN谐波电流动态检测系统。该系统结构简单，算法易实现。仿真研究表明，该系统能在线检测非线性负载的谐波电流，且具有很高的精度，证实了所提方法的有效性。该系统能同时检测多个谐波参数，可广泛应用于电力系统的实时监测，也可检测有源滤波器或有源、无源混合滤波器进行谐波动态补偿时的谐波。

作者简介：危韧勇　男，1962年生，副教授，从事牵引供电系统谐波、无功和不对称综合治理及补偿的研究。
　　　　　李志勇　男，1973年生，硕士研究生，研究方向为智能检测和人工神经元网络技术。
作者单位：长沙铁道学院信息学院，410075 长沙

7　参考文献
1　肖湘宁，徐永梅.电力系统谐波及其综合冶理.中国电力，1998，31(4)
2　张伏生et al.电力系统谐波分析的高精度FFT算法.中国电机工程学报，1999，19(3)
3　Widrow B et al.Adaptive signal processing.Prntics hall,Englewood Cliffs,N j,1985

上一页  [1] [2] 

本文关键字：测量  网络  谐波  神经元  经验交流，电工技术 - 经验交流