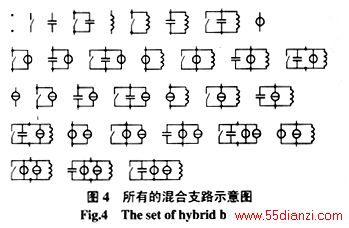
列举出所有的支路组合后，首先根据电路原理检查混合支路的电气合理性，检查原则包括：如果节点i和节点j间连接有电流源，则节点i和节点j间必须至少存在一条通路，这可以称为电流源约束；如果节点i和节点j间连接有电压源，则节点i和节点j间不能存在通路，这可以称为电压源约束。经过判定，可以得出如下结论：① 电压源不可以和开关直接并联；② 电压源与其它元件直接并联，根据电路原理，总能等效为一个电压源。
经过筛选，可以得出有效的混合支路的编号如下：0、1、2、3、4、5、6、7、8、16、17、18、19、20、21、22和23。如图5所示。
（1）矩阵表示方法
对于一个节点数为n的混合开关拓扑，设其任意两节点间最多仅存在1条支路，其邻接矩阵A定义为一个 n×n的方阵，其元素为
式中 m为混合支路的编号。那么，混合开关拓扑的矩阵表述形式为
T=A
与简单图的邻接矩阵相比，可以称之为边加权邻接矩阵。
（2）编号表示方法
在给出了基于混合支路的矩阵表示方法之后，同样可以给出其编号表示方法。在节点数为n的拓扑中，由前假设混合开关拓扑为无自环和复边
式中 aij为n节点网络的邻接矩阵元素，其定义如式(3)所示。
为了表示清晰起见，这里对部分混合支路重新编码，设支路编号16改为编号9、支路编号17编号为A（在邻接矩阵中记为数10），依次编号18为B（在邻接矩阵中记为数11）、19为C（在邻接矩阵中记为数12）、20为D（在邻接矩阵中记为数13）、21为E（在邻接矩阵中记为数14）、22为F（在邻接矩阵中记为数15）和23则为G（在邻接矩阵中记为数16）。这样，D=dmdm-1 dm-2...d2d1d0就构成了一个k位的17进制数，D值的范围是0~17k-1，且D值同该拓扑的邻接矩阵一一对应。根据拓扑的邻接矩阵，可以根据式(4)计算其D值；而每给出一个D，也可以根据式(3)写出其相应的邻接矩阵，并能画出该拓扑的图。这样就用编号的方法完成了对拓扑的描述。
图1所示的拓扑T可以表示为
T=(1813418009)
可以证明，基于单属性网络的矩阵和编号方法的表示混合开关拓扑在进行了电压源判据判定后与基于混合支路描述方法的混合开关拓扑是一一对应的，并可以相互转换。
3 同构混合开关拓扑的判定原理
3.1 简单图同构的概念及其判定方法
设G1和G2是两个简单图，如果存在一个使V(G1)
到V(G2)之间保持相邻性的1-1映射σ，则称G1和G2是同构的，记作
，映射σ称为同构映射。两个同构的图在本质上是一样的，只不过是同一个图的不同画法，同时顶点的编号有可能不同[5]。
如果两个同构图的顶点编号一致，不管它们的画法如何不一样，它们的邻接矩阵是相等的。如果它们的顶点编号不一致，则它们的邻接矩阵之间仅仅是行列次序不同。设A和B分别为同构图G1和G2的邻接矩阵，那么一定存在一系列的置换矩阵P1, P2,..., Pk使得
置换矩阵的定义是由单位矩阵引出的，一个n´n的矩阵E，如果
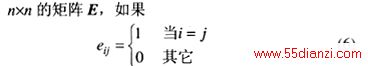
则称矩阵E为单位矩阵。置换矩阵P是由单位矩阵通过行和列的交换得到的。置换矩阵每一行和每一列都只有一个1。一个矩阵右乘置换矩阵，相当于矩阵的列交换运算，左乘置换矩阵相当于矩阵的行交换运算[6]。根据置换矩阵的性质可知P-1= P，式(5)可以表述为
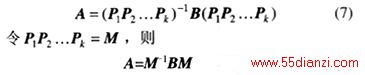
从式(7)中可以看出，如果G1 和G2是同构的，则它们的邻接矩阵是相似的。根据线性代数的知识可以得到，具有相同特征值组的矩阵才是相似的矩阵，所以可以通过检查邻接矩阵的特征值来判定简单图的同构。
3.2 同构混合开关拓扑的判定方法
同构混合开关拓扑的判定，可以借鉴简单图的同构判定方法，需要指出的是使用基于混合支路数学描述方法对于判定同构混合开关拓扑比较方便。
基于混合支路数学描述的混合开关拓扑与简单图的区别在于：在简单图中，如果两个节点之间存在有边，则在邻接矩阵中表示该边的项为1，否则为零；而在混合开关拓扑中，如果节点间存在支路，则在邻接矩阵中表示该支路的项为m（m代表该支路的编号，蕴涵着该支路的具体电路形式），否则为零。也就是说，二者的区别在于其邻接矩阵的每个代表支路元素的权值有所不同，其余都是一样的。
本文关键字：开关 电源，电工技术 - 电源
