微步驱动步进电动机的角速度均匀性
点击数:7610 次 录入时间:03-04 11:57:49 整理:http://www.55dianzi.com 驱动电路及控制电路
)显著减小。而在较高转速范围内,角速度波动的值几乎没有变化。采取微步驱动技术可显著提高步进电动机低速运行的平稳性。
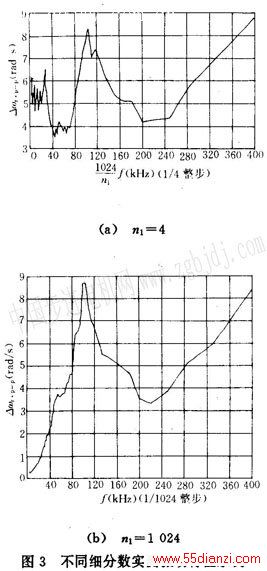
图2c或b表明,微步驱动电动机角速度呈4次谐波的特征,即在一个齿距范围交变4个周期。然而在一个齿距范围内走的步数很多,例如n
1=l 024时一个齿距要走4 096步。可见,对于走步脉冲而言,角速度的波动缓变。在一步范围内可认为角速度不变,即可近似地看成一种准稳态运行,可写成:
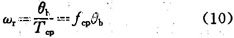
上式表明,在f
cp恒定时,角速度的波动是由步距角的变动,即步距角误差引起的。反之,角速度的波动反映了步距角的变化。
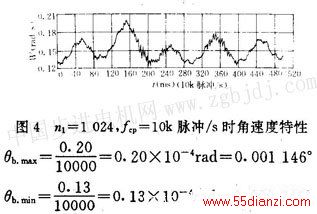
以图4所示实测的角速度曲线为例。从图中可得角速度的最大值约为

=0.20rad/s,最小值约为

=O.13 rad/s。相应地可得步距角的最大值和最小值为:
步距角的平均值:

=0.15×10
-4=0.000 862
o
所以微步距角误差为:

=+O.000 278
o和-0.000 117
o
这和微步距角测试所得结果基本一致。
4结论
a.微步驱动能显著提高步进电动机低速运行区角速度的平稳性。对高速运行域角速度的稳定性没有明显的影响。
b.微步驱动系统低速运转的均匀性主要由微步距角的均匀性决定,对于四相(二相)电动机,减小4次谐波转矩的影响很重要。
c.给出了用角速度变化曲线确定微步距角变化规律和微步距角误差的新方法。
上一页 [1] [2]
本文关键字:电动机 角速度 驱动电路及控制电路,单元电路 - 驱动电路及控制电路
 图2c或b表明,微步驱动电动机角速度呈4次谐波的特征,即在一个齿距范围交变4个周期。然而在一个齿距范围内走的步数很多,例如n1=l 024时一个齿距要走4 096步。可见,对于走步脉冲而言,角速度的波动缓变。在一步范围内可认为角速度不变,即可近似地看成一种准稳态运行,可写成:
图2c或b表明,微步驱动电动机角速度呈4次谐波的特征,即在一个齿距范围交变4个周期。然而在一个齿距范围内走的步数很多,例如n1=l 024时一个齿距要走4 096步。可见,对于走步脉冲而言,角速度的波动缓变。在一步范围内可认为角速度不变,即可近似地看成一种准稳态运行,可写成:
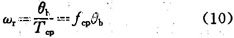 上式表明,在fcp恒定时,角速度的波动是由步距角的变动,即步距角误差引起的。反之,角速度的波动反映了步距角的变化。
以图4所示实测的角速度曲线为例。从图中可得角速度的最大值约为
上式表明,在fcp恒定时,角速度的波动是由步距角的变动,即步距角误差引起的。反之,角速度的波动反映了步距角的变化。
以图4所示实测的角速度曲线为例。从图中可得角速度的最大值约为 =0.20rad/s,最小值约为
=0.20rad/s,最小值约为 =O.13 rad/s。相应地可得步距角的最大值和最小值为:
=O.13 rad/s。相应地可得步距角的最大值和最小值为:
 步距角的平均值:
步距角的平均值:
 =0.15×10-4=0.000 862o
所以微步距角误差为:
=0.15×10-4=0.000 862o
所以微步距角误差为:
 =+O.000 278o和-0.000 117o
这和微步距角测试所得结果基本一致。
4结论
a.微步驱动能显著提高步进电动机低速运行区角速度的平稳性。对高速运行域角速度的稳定性没有明显的影响。
b.微步驱动系统低速运转的均匀性主要由微步距角的均匀性决定,对于四相(二相)电动机,减小4次谐波转矩的影响很重要。
c.给出了用角速度变化曲线确定微步距角变化规律和微步距角误差的新方法。
=+O.000 278o和-0.000 117o
这和微步距角测试所得结果基本一致。
4结论
a.微步驱动能显著提高步进电动机低速运行区角速度的平稳性。对高速运行域角速度的稳定性没有明显的影响。
b.微步驱动系统低速运转的均匀性主要由微步距角的均匀性决定,对于四相(二相)电动机,减小4次谐波转矩的影响很重要。
c.给出了用角速度变化曲线确定微步距角变化规律和微步距角误差的新方法。