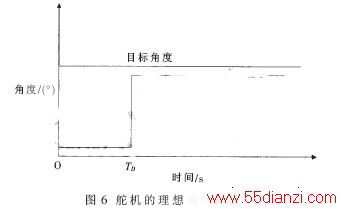
3 转向策略设计
如图7所示,设小车前方距离D处为弯道,小车此刻速度为V,结合图6小车舵机转向理想模型响应曲线,如果让小车在A点入弯,速度必须满足:
D=V×TD (9)
在图4中,对于基准位置1和基准位置2,由道路信息提取的结果,为了保证A点入弯,基准位置2比基准位置1更早地发出转向命令,需要更大的速度才可以在A点入弯,在保证两位置的速度可以安全过弯的前提下,基准位置2得到了更高的入弯速度,所以更早地得到弯道的信息可以提高入弯速度。同时小车要想快速地入弯,必须将基准位置提到一个与此刻速度匹配的位置,才可以抵消舵机延时带来的附加行驶路径。但并不是说只要将基准位置选得足够远就可以得到很大的入弯速度,答案是否定的。小车的转向为一个近似的圆周运动,不同的速度显然对应不同的行驶半径,即不同的路径。速度快时,半径大;速度慢时,半径小。过快的速度会使小车冲出赛道。竞赛赛道的弯道主要由360°、180°、90°、S型赛道组成。在图8所示的180°弯道中,中间的粗实线为引导线,最外围的实线为赛道边界,曲线1、2、3、4为小车行驶路线。设所有行驶路线有同样的入弯角度,曲线1、2、3为B点入弯,速度不同;曲线4为E点入弯,速度与曲线3速度一致。
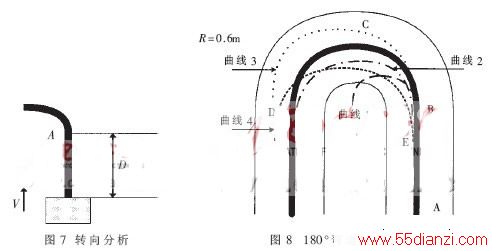
显然,曲线1、2、3中曲线3速度为最快,但路径却最长,同时还有冲出赛道的危险;曲线2虽“抄近道”,但速度稍慢;曲线1由于速度太慢而无法过弯。不难看出,其实曲线2、3、4的过弯时间相差并不是很大。但是由于曲线2中,由直道AB入弯时需要减速,过弯后需加速,这段时间却比曲线3、4来得长。经综合考虑,曲线3、4过弯时间最短。曲线3、4中曲线3很显然有冲出赛道的危险,因此曲线4为过180°弯的最优路径。可以看出,高速时提前入弯可以使小车以一个比较高的速度驶过弯道,同时保证了安全而又不会冲出赛道。
对于90°弯道,与180°类似,最优的策略是为保持直道高速行驶,通过上述的提前入弯策略保证安全过弯。
对于S道的进入,可以类推。而对于S道的行驶则应适当降低车速并将基准位置适当降低。如图9所示,最短路径也为最快速度,两者是统一的。真实过程中很难做到让车走CD路线,但是如果能使舵机保持在一个小角度左右调节的过程中则可逼近CD路线。实践证明,高速通过S道时避免剧烈的角度变化给定为最优策略。

综合以上分析,可以得到以下两点结论:
(1) 基准位置距小车的距离与速度呈正比关系。想要不减速入弯,必须改变基准位置,使之可以满足公式(9)。
(2) 速度与转弯半径呈正比关系。保持高速入弯,同时不冲出赛道,提前入弯策略可以有效解决这个问题。
4 策略的实现
由以上分析可知,场景中的基准位置可以近似看成入弯点,并且不同的速度会导致不同的入弯点,也会导致不同的过弯路径。因此,需完成的控制任务是:高速过弯,在入弯前不减速,为了防止冲出赛道还需要提前入弯。可见,需要在与速度适应的入弯点的基础上进一步提前基准位置,即基准位置离小车的前端距离为:
L=V×TD+V×τ (10)
式中,L为基准位置离小车的距离,V为此刻小车的速度,V×TD为抵消延迟时间带来的附加行驶距离,V×τ为提前入弯点的距离。
可以看出,基准位置与小车的距离是一个与小车速度相关的变量,不同的速度需要不同的取值。对于不同的速度将基准位置按照公式(10)设置,这样即可以实现高速入弯。为了得到较佳的入弯点,本策略对图像平面(64×106)做了进一步的处理,针对已经得到的图像平面(64×106),将图像平面平分为10个区域,每个区域求取引导线的平均位置,对于没有引导线的区域使用一个不可能出现的值代替,这样便将引导线信息简化为10行信息表示,记为:average[i],i=1,2,…,10。其中,average[i]记录每行信息中引导线的平均位置的列坐标值,i标表示行值。图10为最终的图像平面。
www.55dianzi.com
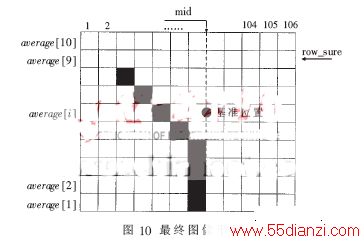
图10中, row_sure(出界点)用来选择10个点中哪几个点为可用点。average[1]为离车最近的点,随着序号增大,离车越远。在图10的图像平面中,计算偏差改为:
err=average[i]-mid (11)
式中, i< P>
当小车车速很高时,选择较远处的点求取偏差,等效于时间上提前入弯。这样由以上策略分析可知,只要入弯点合适,基本不用减速就可以直接入弯,还可以得到不错的安全系数。当速度处于一个较低水平时可使用最近处的点,即average[1],这样就保证车只有走到弯道处才会转向,不会提前入弯,避免提前入弯带来的冲出内道。
5 实验数据
根据比赛要求,赛道中最小弧度半径不小于0.5 m,在参考历届赛道的基础上,笔者设计了如图11的测试赛道,全长约38 m。实验室测试成绩为18 s跑完全程,平均速度达到2 m/s。

图12为90°弯道过弯图,粗实线为引导线,虚线为赛车实际行驶路线。可以看出,小车实现了提前入弯,这是比较好的路径,有效地节省了时间。

过弯速度的测量,由无线模块每40 ms发回编码器测得的速度脉冲,先由直道加速后入弯得到如表1所示的数据。

由表1可以明显看出速度的变化,其中62为入弯速度,折合成标准速度为2.4 m/s;弯道速度为40,折合成标准速度为1.5 m/s,这个速度很接近平均速度。
图13为360°弯道过弯图,粗实线为引导线,虚线为小车实际的行驶路线。可以看出实现了提前入弯,后半程受舵机最大偏转角的限制,无法继续加大偏转,造成有一些跑外道。
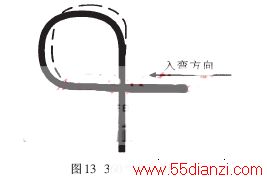
图14为S过弯图,粗实线为引导线,虚线为小车实际的行驶路线。可以看出,小车行驶路线已经很逼近直道了,由无线模块每40 ms发回编码器测得的速度脉冲,先由直道加速后入弯得到如表2所示的数据。


可以看出,S道的速度变化很小,同时弯道速度平均在1.5 m/s以上,很好地逼近了预期的路线。
本文根据转向模型,通过分析过弯路径与过弯速度之间的关系,得到了不同速度对应不同入弯路径和入弯点的结论。利用这个结论,改变控制器偏差计算,达到动态地设置入弯点,快速入弯,尽量做到不减速或少减速,缩短弯道行驶时间,从而提高小车行驶速度的目的。该方法在其他智能车跟随引导线的系统中同样适用,由于其良好的超前预测性能,对于短暂的引导线丢失也可以很好地跟随。
本文关键字:智能 机器人-智能车,电子知识资料 - 机器人-智能车